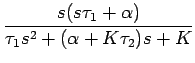Sous-sections
La boucle à verrouillage de phase (Phase-Locked Loop
en anglais ou PLL) est un système largement utilisé
pour la détection et la démodulation de signaux modulés. Le principe
de la boucle à verrouillage de phase consiste à suivre les variations
de phase du signal d'entrée et à fournir en sortie un signal dépendant
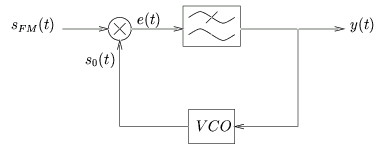
du taux de variation de la phase d'entrée. Le schéma d'une boucle
utilisée pour la démodulation FM est repris à la figure 3.26.
Figure 3.26:
Utilisation d'une boucle à verrouillage de phase pour la démodulation
FM [1].
|
|
L'entrée de la boucle à verrouillage de phase est un signal FM dont
la forme est
sFM(t) = Accos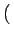 2 2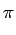 fct + fct + 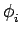 (t) (t)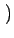 |
(3.85) |
La phase instantanée
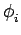 (t) est reliée au signal modulant
m(t) par
(t) est reliée au signal modulant
m(t) par
ou encore
m(t) = 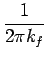 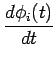 |
(3.87) |
La PLL est articulée autour d'un oscillateur contrôlé en tension (Voltage-Control
Oscillator ou VCO) dont la fréquence est proportionnelle au
signal d'entrée. La sortie du VCO est une sinusoïde de la forme
s0(t) = B sin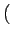 2 2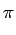 fct + fct + 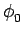 (t) (t)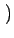 |
(3.88) |
En régime, la phase
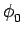 (t) du signal produit localement est
liée à la sortie y(t) de la PLL par la relation
(t) du signal produit localement est
liée à la sortie y(t) de la PLL par la relation
soit encore
y(t) = 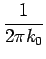 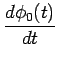 |
(3.90) |
Si
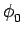 (t)
(t) 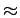
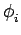 (t),
y(t)
(t),
y(t) 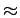 m(t)(kf/k0)
est le signal démodulé à une constante multiplicative près. En d'autres
termes, la PLL se comporte comme un dérivateur idéal.
m(t)(kf/k0)
est le signal démodulé à une constante multiplicative près. En d'autres
termes, la PLL se comporte comme un dérivateur idéal.
La boucle à verrouillage de phase est constituée d'un mélangeur et
d'un filtre passe-bas éliminant les fréquences supérieures à 2fc.
Le signal d'erreur e(t) à la sortie du mélangeur vaut
| e(t) |
= |
sFM(t)s0(t) |
(3.91) |
| |
= |
AcB sin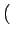 2 2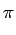 fct + fct + 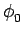 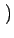 cos cos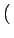 2 2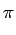 fct + fct + 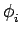 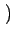 |
(3.92) |
| |
= |
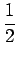 AcB AcB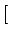 sin sin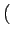 4 4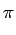 fct + fct + 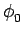 + + 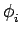 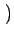 + sin + sin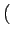 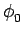 - - 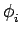 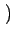 ![$\displaystyle \left.\vphantom{\sin\left(4\pi f_{c}t+\phi_{0}+\phi_{i}\right)+\sin\left(\phi_{0}-\phi_{i}\right)}\right]$](img294.gif) |
(3.93) |
Si les signaux
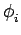 (t) et
(t) et
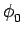 (t) varient lentement
par rapport à
2
(t) varient lentement
par rapport à
2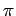 fct, la sortie du filtre passe-bas est donnée
par
fct, la sortie du filtre passe-bas est donnée
par
y(t) = 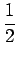 AcB sin AcB sin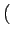 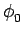 - - 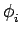 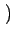 = - = - 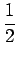 AcB sin AcB sin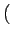 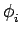 - - 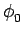 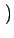 |
(3.94) |
Comme
d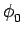 /dt = 2
/dt = 2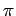 k0y(t), nous obtenons l'équation différentielle
non-linéaire suivante:
k0y(t), nous obtenons l'équation différentielle
non-linéaire suivante:
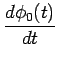 = - = - 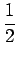 AcB(2 AcB(2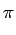 k0)sin k0)sin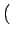 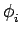 (t) - (t) - 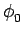 (t) (t)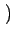 = K sin = K sin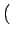 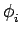 (t) - (t) - 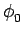 (t) (t)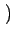 |
(3.95) |
où
K = - 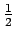 AcB(2
AcB(2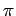 k0). Le système est dit synchronisé
ou verrouillé si
k0). Le système est dit synchronisé
ou verrouillé si
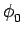
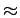
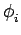 . Dans ce cas, nous
avons l'approximation linéaire suivante:
. Dans ce cas, nous
avons l'approximation linéaire suivante:
Ce modèle linéaire peut être étudié facilement via la transformée
de LAPLACE. Nous obtenons ainsi la relation
ou encore
Comme
d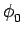 /dt = 2
/dt = 2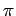 k0y(t) et
d
k0y(t) et
d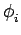 /dt = 2
/dt = 2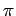 kfm(t),
nous avons
kfm(t),
nous avons
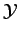 (s) = s
(s) = s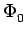 (s)/(2
(s)/(2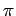 k0) et
k0) et
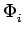 (s) = 2
(s) = 2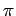 kf
kf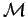 (s)/s.
Nous obtenons ainsi
(s)/s.
Nous obtenons ainsi
et
Pour la démodulation du signal FM, il serait intéressant d'avoir
y(t) 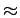 m(t)
ou
m(t)
ou
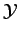 (s)
(s) 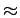
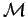 (s). Si K
(s). Si K 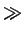 1, nous avons
1, nous avons
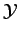 (s)
(s) 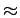 (kf/k0)
(kf/k0)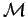 (s) et la démodulation
est satisfaisante. Il est important de remarquer que ce résultat est
valable uniquement si la PLL est verrouillée sur la phase du signal
FM ou lorsque l'erreur de phase
(s) et la démodulation
est satisfaisante. Il est important de remarquer que ce résultat est
valable uniquement si la PLL est verrouillée sur la phase du signal
FM ou lorsque l'erreur de phase
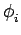 -
- 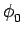 est petite. Si
cette erreur est trop importante, le signal de sortie subit des distorsions.
Naturellement, durant la phase d'acquisition, l'erreur de phase est
trop grande pour que le modèle linéaire soit acceptable.
est petite. Si
cette erreur est trop importante, le signal de sortie subit des distorsions.
Naturellement, durant la phase d'acquisition, l'erreur de phase est
trop grande pour que le modèle linéaire soit acceptable.
Sous condition de verrouillage, un modèle général à contre-réaction
peut être développé pour la PLL. Ce modèle est montré à la figure 3.27.
À nouveau, l'objectif est de suivre la phase instantanée
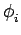 (t)
du signal d'entrée. Le bloc de contre-réaction K/s décrit l'effet
du VCO et produit une phase qui varie avec y(t). En fonctionnement
linéaire, la sortie du détecteur (mélangeur et filtre passe-bas) est
approximativement égale à
(t)
du signal d'entrée. Le bloc de contre-réaction K/s décrit l'effet
du VCO et produit une phase qui varie avec y(t). En fonctionnement
linéaire, la sortie du détecteur (mélangeur et filtre passe-bas) est
approximativement égale à
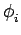 -
- 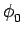 et son effet est modélisé
par la sommation du schéma.
et son effet est modélisé
par la sommation du schéma.
Figure 3.27:
Modèle de PLL à contre-réaction.
|
|
Nous obtenons les fonctions de transfert suivantes
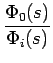 = = 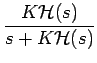 |
(3.102) |
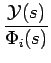 = = 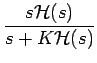 |
(3.103) |
La fonction de transfert de l'erreur de phase, définie par
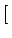
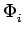 (s) -
(s) - 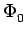 (s)
(s)![$ \left.\vphantom{\Phi_{i}(s)-\Phi_{0}(s)}\right]$](img319.gif) /
/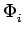 (s),
est donnée par
(s),
est donnée par
Pour un gain en boucle ouverte important (
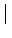 K
K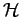 (s)
(s)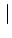
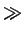 1),
nous avons
1),
nous avons
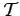 (s) =
(s) = 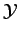 (s)/
(s)/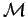 (s)
(s) 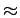 1,
et le signal de sortie y(t) est égal au signal modulant m(t).
Si la phase d'entrée
1,
et le signal de sortie y(t) est égal au signal modulant m(t).
Si la phase d'entrée
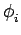 (t) ne varie pas, le signal d'erreur
(t) ne varie pas, le signal d'erreur
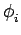 (t) -
(t) - 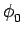 (t) est nul, ainsi que le signal de sortie.
(t) est nul, ainsi que le signal de sortie.
Le bloc
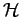 (s) de la figure 3.27
peut être réalisé par un filtre actif ou passif. Si
(s) de la figure 3.27
peut être réalisé par un filtre actif ou passif. Si
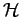 (s) = 1,
nous obtenons une boucle du premier ordre avec
(s) = 1,
nous obtenons une boucle du premier ordre avec
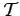 (s) = K/(s + K).
Sa réponse fréquentielle (régime établi) ainsi que l'erreur de phase
peuvent respectivement s'écrire
(s) = K/(s + K).
Sa réponse fréquentielle (régime établi) ainsi que l'erreur de phase
peuvent respectivement s'écrire
et
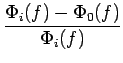 = = 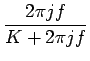 |
(3.106) |
Le gain K de la boucle caractérise complètement la réponse de la
boucle fermée. Si
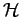 (s) est un système du premier ordre
de la forme
(s) est un système du premier ordre
de la forme
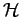 (s) = (s
(s) = (s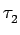 +1)/(s
+1)/(s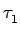 +
+ 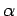 ), nous
obtenons une boucle du second ordre dont la réponse fréquentielle
et l'erreur de phase sont données par
), nous
obtenons une boucle du second ordre dont la réponse fréquentielle
et l'erreur de phase sont données par
Les paramètres K, 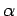 ,
, 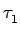 et
et 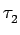 sont choisis
afin de maintenir l'erreur de phase la plus faible possible tout en
minimisant les distorsions sur le signal de sortie.
sont choisis
afin de maintenir l'erreur de phase la plus faible possible tout en
minimisant les distorsions sur le signal de sortie.
La boucle à verrouillage de phase est un circuit fondamental. Son
fonctionnement est de type analogique. Actuellement, il existe des
boucles entièrement numériques qui réalisent la même fonction.
Elles procèdent par échantillonnage et stockage des signaux.
Marc Van Droogenbroeck. Tous droits réservés.
2005-03-11
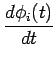
![]() (t) du signal produit localement est
liée à la sortie y(t) de la PLL par la relation
(t) du signal produit localement est
liée à la sortie y(t) de la PLL par la relation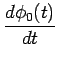
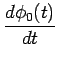 = -
= - 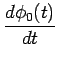
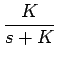
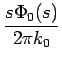 =
= 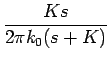
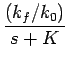 K
K![]() (t)
du signal d'entrée. Le bloc de contre-réaction K/s décrit l'effet
du VCO et produit une phase qui varie avec y(t). En fonctionnement
linéaire, la sortie du détecteur (mélangeur et filtre passe-bas) est
approximativement égale à
(t)
du signal d'entrée. Le bloc de contre-réaction K/s décrit l'effet
du VCO et produit une phase qui varie avec y(t). En fonctionnement
linéaire, la sortie du détecteur (mélangeur et filtre passe-bas) est
approximativement égale à
![]() -
- ![]() et son effet est modélisé
par la sommation du schéma.
et son effet est modélisé
par la sommation du schéma.
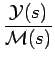 =
= 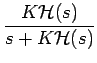
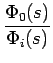 =
= 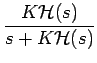
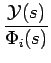 =
= 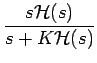
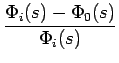 = 1 -
= 1 - 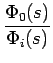 =
= 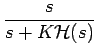
![]() (s) de la figure 3.27
peut être réalisé par un filtre actif ou passif. Si
(s) de la figure 3.27
peut être réalisé par un filtre actif ou passif. Si
![]() (s) = 1,
nous obtenons une boucle du premier ordre avec
(s) = 1,
nous obtenons une boucle du premier ordre avec
![]() (s) = K/(s + K).
Sa réponse fréquentielle (régime établi) ainsi que l'erreur de phase
peuvent respectivement s'écrire
(s) = K/(s + K).
Sa réponse fréquentielle (régime établi) ainsi que l'erreur de phase
peuvent respectivement s'écrire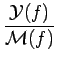 =
= 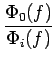 =
= 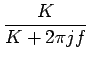
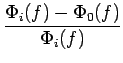 =
= 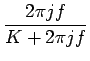
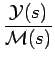 =
= 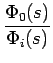 =
= 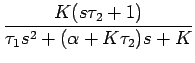
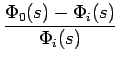 =
= 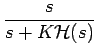 =
=