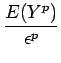Le résultat d'une expérience aléatoire n'étant pas déterministe, il
convient de caractériser le comportement moyen des résultats
d'une expérience aléatoire par des outils appropriés. Pour ce faire,
nous introduisons quelques définitions.
Définition 28
Le n-ième moment de la variable aléatoire X est défini par
où
E
 désigne l'opérateur d'espérance statistique.
désigne l'opérateur d'espérance statistique.
Les deux premiers moments de la variable aléatoire X sont les plus
importants. Considérons tout d'abord l'équation 4.23
pour n = 1.
Définition 29
[Moyenne]
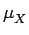 est appelée espérance ou moyenne de
la variable aléatoire X.
est appelée espérance ou moyenne de
la variable aléatoire X.
La moyenne 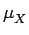 est située au centre de gravité de l'aire
située sous la courbe de la fonction de densité de probabilité de
X. Considérons maintenant l'équation 4.23 pour n = 2.
est située au centre de gravité de l'aire
située sous la courbe de la fonction de densité de probabilité de
X. Considérons maintenant l'équation 4.23 pour n = 2.
E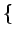 X2
X2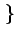 représente la moyenne du carré de la variable
X, à ne pas confondre avec le carré de la moyenne
représente la moyenne du carré de la variable
X, à ne pas confondre avec le carré de la moyenne
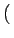 E
E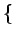 X
X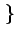
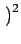 =
= 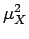 .
.
Pour n = 1, le moment centré est évidemment égal à zéro, tandis que
pour n = 2, nous obtenons le moment centré d'ordre 2 aussi appelé
variance de la variable aléatoire X.
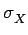 , la racine carrée de la variance est appelée écart-type
de la variable aléatoire X. La variance
, la racine carrée de la variance est appelée écart-type
de la variable aléatoire X. La variance
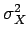 de la
variable aléatoire X est en quelque sorte une mesure de l'aspect
aléatoire de la variable. En spécifiant la variance
de la
variable aléatoire X est en quelque sorte une mesure de l'aspect
aléatoire de la variable. En spécifiant la variance
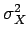 ,
nous limitons la largeur effective de la fonction de densité
de probabilité fX(x) autour de la moyenne
,
nous limitons la largeur effective de la fonction de densité
de probabilité fX(x) autour de la moyenne 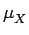 .
.
Une description précise de cette limite a été donnée par CHEBYSHEV.
Théorème 32
[CHEBYSHEV [3, page 177]]
Si Y est une variable aléatoire positive, alors pour tout
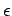 > 0
et
0 < p < +
> 0
et
0 < p < +  ,
,
Sous une forme particulière, on a
Nous voyons donc que la moyenne et la variance d'une variable aléatoire
donnent une description partielle de sa distribution de probabilité.
Finalement, nous tirons de 4.27 que la variance et la
moyenne du carré de la variable sont liées par la relation
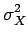 |
= |
E X2 -2 X2 -2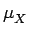 X + X + 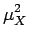  |
|
| |
= |
E X2 X2 -2 -2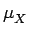 E E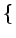 X X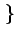 + + 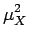 |
|
| |
= |
E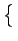 X2 X2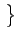 - - 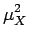 |
|
dans laquelle nous avons utilisé le fait que l'opérateur d'espérance
statistique E est linéaire.
Marc Van Droogenbroeck. Tous droits réservés.
2005-03-11
![]() X2
X2![]() représente la moyenne du carré de la variable
X, à ne pas confondre avec le carré de la moyenne
représente la moyenne du carré de la variable
X, à ne pas confondre avec le carré de la moyenne
![]() E
E![]() X
X![]()
![]() =
= ![]() .
.