Table des matières of 4.3.3 Liens entre moments centrés ou non

4.3.3 Liens entre moments centrés ou non

Proposition 33 [3, page 135] Les moments centrés d'ordre n sont entièrement déterminés par les moments d'ordre k tels que k 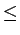$\leq$ n.

Démonstration

L'extension binomiale permet d'écrire la relation

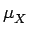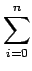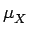(X - $\displaystyle \mu_{{X}}^{}$ )ⁿ = $\displaystyle \sum_{{i=0}}^{{n}}$ C_iⁿXⁱ(- $\displaystyle \mu_{{X}}^{}$ )^n-i

(4.30)

Dès lors, par linéarité de l'espérance,

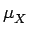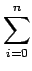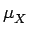E{(X - $\displaystyle \mu_{{X}}^{}$ )ⁿ} = $\displaystyle \sum_{{i=0}}^{{n}}$ C_iⁿ(- $\displaystyle \mu_{{X}}^{}$ )^n-iE{Xⁱ}

(4.31)

Proposition 34 Les moments d'ordre n sont entièrement déterminés par les moments centrés d'ordre k tels que k 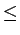$\leq$ n.

Démonstration

Par la proposition précédente et en prenant Xⁿ = (X - 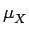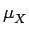$\mu_{{X}}^{}$ + $\mu_{{X}}^{}$ )ⁿ

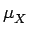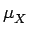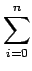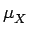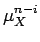E{Xⁿ} = E{(X - $\displaystyle \mu_{{X}}^{}$ + $\displaystyle \mu_{{X}}^{}$ )ⁿ} = $\displaystyle \sum_{{i=0}}^{{n}}$ C_iⁿE{(X - $\displaystyle \mu_{{X}}^{}$ )ⁱ} $\displaystyle \mu_{{X}}^{{n-i}}$

(4.32)

4.3.3.1 Variable aléatoire centrée

En rapport avec la moyenne et la variance, on associe à la variable aléatoire X, la variable aléatoire centrée X_c et la variable aléatoire réduite X_r définies respectivement par:

X_c = X - E{X}

(4.33)

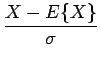X_r = $\displaystyle {\frac{{X-E\{ X\}}}{{\sigma}}}$

(4.34)

4.3.3.2 Fonction caractéristique

Il est parfois plus facile de calculer les moments par le biais d'une représentation spectrale de la densité de probabilité; cela conduit à la définition de la fonction caractéristique.

Définition 35 La fonction caractéristique 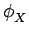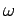$\phi_{{X}}^{}$ ( $\omega$ ) d'une variable aléatoire X est définie par

$\displaystyle \phi_{{X}}^{}$ ( $\displaystyle \omega$ ) = $\displaystyle \int_{{-\infty}}^{{+\infty}}$ f_X(x)e^jxdx

(4.35)

Par transformée inverse, il est possible de retrouver la fonction de densité de probabilité de X à partir de sa fonction caractéristique:

f_X(x) = $\displaystyle {\frac{{1}}{{2\pi}}}$ $\displaystyle \int_{{-\infty}}^{{+\infty}}$ $\displaystyle \phi_{{X}}^{}$ ( $\displaystyle \omega$ )e^-jxd $\displaystyle \omega$

(4.36)