Une variable aléatoire X présente une densité de probabilité uniforme sur l'intervalle (a, b) si
La fonction de répartition de X est alors donnée par
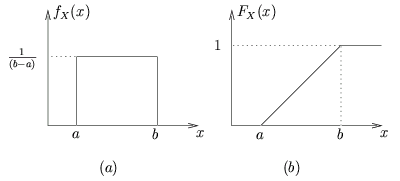
La figure 4.2 montre le graphe de ces deux fonctions.
Soit X une variable aléatoire discrète. La variable X présente une densité binomiale d'ordre n si elle peut prendre les valeurs 0, 1, ..., n de telle sorte que
où
Cnk =  |
(4.40) |
La fonction de densité de probabilité de X est donnée par
La fonction de répartition de X est une fonction en escaliers donnée par
La loi binomiale est utilisée pour le dénombrement d'événements.
Soit X une variable aléatoire discrète. La variable X présente une densité de POISSON, avec un paramètre
La fonction de densité de probabilité de X est donnée par
Comme pour la variable binomiale, la fonction de répartition est une fonction en escalier.
Soit X une variable aléatoire de moyenne
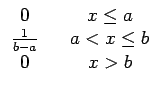
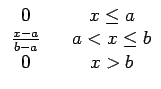
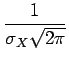 e-
e-