Ce bruit, encore appelé JOHNSON noise, est dû à l'agitation des électrons dans un conducteur, sous l'effet de l'activation thermique. On sait que cette agitation croît avec la température; il en résultera un terme de bruit proportionnel à la température.
Pour des raisons pratiques, on modélise le bruit thermique par la
valeur quadratique moyenne de la tension VBT de bruit thermique
qui apparaît aux bornes d'une résistance, mesurée dans la bande de
fréquences
![]() f [Hz], telle que fournie par
f [Hz], telle que fournie par
| E{VBT2} = 4kBTR |
(4.161) |
En raison de la présence d'un très grand nombre d'électrons dont le mouvement est indépendant, le théorème de la limite centrale conduit à considérer le bruit thermique comme gaussien de moyenne nulle; d'où une densité de probabilité de la forme
p(x) = 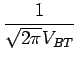 e e |
(4.162) |
Pour déterminer la puissance de bruit produite par la résistance,
il faut considérer l'adaptation de la source de THÉVENIN,
flanquée de sa résistance interne, par rapport à la résistance de
la charge connectée à ses bornes. Le transfert maximum de puissance
a lieu pour une résistance de charge égale à la résistance interne.
Dans ce cas, on détermine une puissance de bruit disponible
de
kBT![]() f [W].
f [W].
À la température ambiante (
T = 300 [K]), la puissance de bruit
disponible vaut
4, 14×10-21![]() f [W]. Aux bornes
d'une résistance de
1 [k
f [W]. Aux bornes
d'une résistance de
1 [k![]() ] et pour une bande de fréquences
de 1 [GHz], elle correspond à une tension de
] et pour une bande de fréquences
de 1 [GHz], elle correspond à une tension de
![]() = 64 [
= 64 [![]() V].
Cette tension est négligeable pour des systèmes numériques en raison
d'autres effets de l'ordre du millivolt. Il en va autrement pour des
récepteurs radio qui fonctionnent avec des niveaux de tension de cet
ordre. Il en résulte qu'on ne peut pas négliger les effets des bruits
thermiques lors de la conception des systèmes radio ou de l'analyse
des performances des techniques de modulation continue.
V].
Cette tension est négligeable pour des systèmes numériques en raison
d'autres effets de l'ordre du millivolt. Il en va autrement pour des
récepteurs radio qui fonctionnent avec des niveaux de tension de cet
ordre. Il en résulte qu'on ne peut pas négliger les effets des bruits
thermiques lors de la conception des systèmes radio ou de l'analyse
des performances des techniques de modulation continue.