Table des matières of 4.6.5 Décomposition de RICE

Ce signal peut aussi être écrit sous la forme de deux composantes dont la première est en phase, composante I, et la seconde en quadrature de phase, composante Q:

s_I(t)	=	A(t)cos $\displaystyle \phi$	(4.179)
s_Q(t)	=	A(t)sin $\displaystyle \phi$	(4.180)

s(t) = A(t)cos(2 $\displaystyle \pi$ f_ct + $\displaystyle \phi$ (t)) = s_I(t)cos(2 $\displaystyle \pi$ f_ct) - s_Q(t)sin(2 $\displaystyle \pi$ f_ct)

(4.181)

En d'autres termes, l'amplitude des composantes modulées I/Q dépend du temps, même lorsque l'enveloppe du signal modulé, A(t), est constante comme c'est le cas pour le GSM.

Une autre interprétation permet de traiter les composantes comme deux signaux modulés en amplitude à porteuse supprimée. Pour un signal s(t) à bande limitée, la décomposition de RICE mène à deux composantes en quadrature indépendantes et en bande de base.

4.6.5.1 Décomposition de RICE d'un bruit blanc à bande étroite

Il est intéressant de calculer, à titre d'illustration, la fonction d'autocorrélation de la décomposition de RICE d'un bruit à bande étroite, et de la comparer au résultat précédent.

Soient n_I(t) et n_Q(t) des processus de bruit indépendants et de densité spectrale $\gamma$ (f )= N₀ pour $\left\vert\vphantom{f}\right.$ f $\left.\vphantom{f}\right\vert$ < ${\frac{{B}}{{2}}}$ , tels qu'ils définissent

n(t) = n_I(t)cos(2 $\displaystyle \pi$ f_ct) - n_Q(t)sin(2 $\displaystyle \pi$ f_ct)

(4.182)

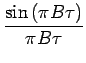$\displaystyle \Gamma_{{N_{I}N_{I}}}^{}$ $\displaystyle \left(\vphantom{\tau}\right.$ $\displaystyle \tau$ $\displaystyle \left.\vphantom{\tau}\right)$ = $\displaystyle \Gamma_{{N_{Q}N_{Q}}}^{}$ $\displaystyle \left(\vphantom{\tau}\right.$ $\displaystyle \tau$ $\displaystyle \left.\vphantom{\tau}\right)$ = BN₀ $\displaystyle {\frac{{\sin\left(\pi B\tau\right)}}{{\pi B\tau}}}$

(4.183)

$\displaystyle \Gamma_{{NN}}^{}$ $\displaystyle \left(\vphantom{\tau}\right.$ $\displaystyle \tau$ $\displaystyle \left.\vphantom{\tau}\right)$	=	E{n(t)n(t - $\displaystyle \tau$ )}	(4.184)
	=	E{n_I(t)n_I(t - $\displaystyle \tau$ )}cos(2 $\displaystyle \pi$ f_ct)cos(2 $\displaystyle \pi$ f_ct - 2 $\displaystyle \pi$ f_c $\displaystyle \tau$ )
		+ E{n_Q(t)n_Q(t - $\displaystyle \tau$ )}sin(2 $\displaystyle \pi$ f_ct)sin(2 $\displaystyle \pi$ f_ct - 2 $\displaystyle \pi$ f_c $\displaystyle \tau$ )
		- E{n_I(t)n_Q(t - $\displaystyle \tau$ )}cos(2 $\displaystyle \pi$ f_ct)sin(2 $\displaystyle \pi$ f_ct - 2 $\displaystyle \pi$ f_c $\displaystyle \tau$ )
		- E{n_Q(t)n_I(t - $\displaystyle \tau$ )}sin(2 $\displaystyle \pi$ f_ct)cos(2 $\displaystyle \pi$ f_ct - 2 $\displaystyle \pi$ f_c $\displaystyle \tau$ )	(4.185)
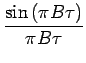	=	BN₀ $\displaystyle {\frac{{\sin\left(\pi B\tau\right)}}{{\pi B\tau}}}$ [cos(2 $\displaystyle \pi$ f_ct)cos(2 $\displaystyle \pi$ f_ct - 2 $\displaystyle \pi$ f_c $\displaystyle \tau$ )
		+sin(2 $\displaystyle \pi$ f_ct)sin(2 $\displaystyle \pi$ f_ct - 2 $\displaystyle \pi$ f_c $\displaystyle \tau$ )]	(4.186)
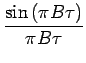	=	BN₀ $\displaystyle {\frac{{\sin\left(\pi B\tau\right)}}{{\pi B\tau}}}$ cos(2 $\displaystyle \pi$ f_c $\displaystyle \tau$ )	(4.187)

Cette dernière expression correspond bien à la fonction d'autocorrélation d'un bruit blanc à bande étroite. Remarquons également que chaque composante en bande de base contient autant de puissance que la décomposition de RICE de n(t). En effet,

4.6.5 Décomposition de RICE

4.6.5.1 Décomposition de RICE d'un bruit blanc à bande étroite

Notes