L'étude des doublets est intéressante car elle éclaire le fonctionnement des mécanismes de calculs des champs.
En plus de leur fonction de guide d'onde, une ligne non blindée ou un micro-ruban rayonnent une partie de leur énergie dans l'air. Il ne s'agira pas pour autant de s'en servir comme antenne car leurs propriétés au rayonnement ne le justifient pas. On peut usiner des structures métalliques ou diélectriques de manière à rayonner efficacement dans l'air avec, en plus, la possibilité de définir des directions privilégiées.
Le doublet électrique ou doublet de HERTZ constitue une structure
d'antenne simplifiée: un élément de courant infinitésimal de longueur
dl est parcouru par un courant décrit par le phaseur ![]() supposé constant (en amplitude et en phase) sur toute sa longueur.
La figure 5.1 montre un doublet placé dans
un système d'axes cartésien et sphérique.
supposé constant (en amplitude et en phase) sur toute sa longueur.
La figure 5.1 montre un doublet placé dans
un système d'axes cartésien et sphérique.
L'antenne raccordée à un doublet générateur crée des ondes électromagnétiques en tout point d'observation P repéré par une distance r définie par rapport à l'origine. Si le doublet est aligné sur l'axe z, le potentiel vecteur se réduit à
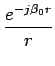 |
(5.26) |
En coordonnées sphériques, on en déduit
| = | 0 | (5.27) | |
| = | 0 | (5.28) | |
| = | (5.29) |
Quant au champ électrique, il vaut
| = | 2 |
(5.30) | |
| = | (5.31) | ||
| = | 0 | (5.32) |
où
![]() =
= ![]() = 120
= 120![]() = 377 [
= 377 [![]() ]
est l'impédance intrinsèque du vide. Remarquons que
]
est l'impédance intrinsèque du vide. Remarquons que
![]() r = 2
r = 2![]() (r/
(r/![]() ),
ce qui définit une sorte de longueur électromagnétique de rayonnement
normalisée.
),
ce qui définit une sorte de longueur électromagnétique de rayonnement
normalisée.
Dans un système de coordonnées sphériques dont l'axe ![]() = 0 est
orienté parallèlement au doublet, le doublet rayonne un champ magnétique
avec une polarisation orientée selon les petits cercles. L'amplitude
du champ rayonné varie en fonction de la direction comme
sin
= 0 est
orienté parallèlement au doublet, le doublet rayonne un champ magnétique
avec une polarisation orientée selon les petits cercles. L'amplitude
du champ rayonné varie en fonction de la direction comme
sin![]() .
Elle se compose d'un terme en 1/r et d'un autre en 1/r2.
Leurs valeurs en amplitude sont égales lorsque
r = 1/
.
Elle se compose d'un terme en 1/r et d'un autre en 1/r2.
Leurs valeurs en amplitude sont égales lorsque
r = 1/![]()
![]()
![]() /6.
À grande distance, notée R, le terme en 1/r contribue principalement
au champ magnétique -c'est l'hypothèse dite du champ
éloigné-; on obtient alors
/6.
À grande distance, notée R, le terme en 1/r contribue principalement
au champ magnétique -c'est l'hypothèse dite du champ
éloigné-; on obtient alors
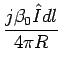 sin sin |
(5.33) |
Sous la même hypothèse de champ éloigné, le champ électrique vaut
| 0 | (5.34) | ||
| = | 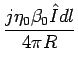 sin sin |
(5.35) |
La puissance rayonnée (phasorielle) est fournie par le vecteur de POYNTING:
| (5.37) |
Après calcul, on obtient
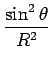 |
(5.38) |
Ainsi, la puissance émise par unité de surface est dirigée le long de l'axe reliant le doublet au point d'observation.
Directivité et gain. On utilise souvent des représentations
graphiques pour exprimer la directivité d'une antenne par un diagramme
de rayonnement. Ce diagramme peut être représenté sous diverses formes.
Ce diagramme représente l'intensité du champ électrique ou la densité
de puissance pour différents angles d'observation par rapport à l'antenne.
On parle de diagramme de rayonnement absolu s'il est exprimé
en termes d'intensité électrique
![]() ou de densité de puissance
ou de densité de puissance
![]() . S'il est défini par rapport à une puissance de référence,
on obtient le diagramme de rayonnement relatif5.2.
. S'il est défini par rapport à une puissance de référence,
on obtient le diagramme de rayonnement relatif5.2.
Une forme commune du diagramme de rayonnement est la représentation
polaire qui donne la forme de la zone de portée de l'antenne. Le diagramme
peut être composé d'un lobe principal et de lobes secondaires; dans
ce cas, un paramètre définissant assez bien la directivité de l'antenne
est l'angle d'ouverture du lobe principal à 3 [dB],
![]() .
Il est illustré à la figure 5.2.
.
Il est illustré à la figure 5.2.
Il est évident qu'une antenne directive économise la puissance de l'émetteur en concentrant celle-ci dans une direction préférentielle et apporte un gain. Intuitivement, on définit le gain dans une direction comme le rapport du vecteur de POYNTING dans cette direction à celui d'une antenne à rayonnement isotrope rayonnant la même puissance.
Revenons au doublet de HERTZ. Pour une distance R fixée,
on peut dessiner une figure tridimensionnelle de l'amplitude de la
puissance moyenne rayonnée; il s'agit du diagramme de rayonnement
qui caractérise les propriétés de l'antenne au rayonnement et ses
capacités à émettre dans une direction donnée. La figure 5.3
reprend le diagramme de rayonnement du doublet électrique. On remarquera
la symétrie dans le plan de l'équateur et la dépendance en
sin![]() .
.
La puissance totale rayonnée est l'intégrale de
![]() sur
une surface incluant le doublet. En choisissant une sphère de rayon
R, on obtient5.3
sur
une surface incluant le doublet. En choisissant une sphère de rayon
R, on obtient5.3
Résistance de rayonnement. La résistance fictive de rayonnement est le rapport de la puissance rayonnée par l'antenne et du carré de l'intensité du courant (exprimé en valeur efficace si le courant est représenté par un phaseur) alimentant l'antenne
| Rr = |
(5.41) |
C'est la résistance qui, en lieu et place de l'antenne, dissiperait
la même puissance que la puissance rayonnée par l'antenne. Par l'équation 5.40,
on calcule une résistance équivalente au rayonnement valant
80![]()
![]()
![]()
![]() .
Cette résistance représente une résistance fictive qui dissipe la
même puissance qu'émet un doublet électrique. Les performances du
doublet sont cependant médiocres. Par exemple, pour un doublet de
longueur dl = 1 [cm] et une fréquence de
300 [MHz] (
.
Cette résistance représente une résistance fictive qui dissipe la
même puissance qu'émet un doublet électrique. Les performances du
doublet sont cependant médiocres. Par exemple, pour un doublet de
longueur dl = 1 [cm] et une fréquence de
300 [MHz] (
![]() = 1
[m]), la résistance équivalente vaut
79 [m
= 1
[m]), la résistance équivalente vaut
79 [m![]() ]. Pour rayonner
une puissance de 1 [W], il faut donc un courant de 3, 6 [A]!
]. Pour rayonner
une puissance de 1 [W], il faut donc un courant de 3, 6 [A]!
Un calcul équivalent à celui du doublet de HERTZ peut être mené pour une boucle parcourue par un courant. La structure ainsi obtenue porte le nom de doublet magnétique (cf. figure 5.4).
Son rayonnement est également médiocre. On peut ainsi montrer que le vecteur de POYNTING vaut, en champ éloigné,
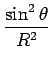 |
(5.42) |
| Prad | = | (5.43) | |
| = | 15, 585 |
(5.44) |
À nouveau, pour une boucle de courant de rayon égal à 1 [cm] et
une fréquence de 300 [MHz] (
![]() = 1 [m]), la résistance
équivalente vaut
3, 08 [m
= 1 [m]), la résistance
équivalente vaut
3, 08 [m![]() ]. Pour rayonner une puissance de
1 [W], il faut à cette fois un courant de 18 [A]!
]. Pour rayonner une puissance de
1 [W], il faut à cette fois un courant de 18 [A]!
La raison pour laquelle le doublet de HERTZ rayonne mal tient en partie à sa petite longueur. Le remède imaginé a consisté à allonger le dipôle.
Le principe de fonctionnement intuitif est celui d'une ligne parallèle dont on écarterait progressivement les conducteurs, tel que représenté à la figure 5.5.
Des ondes de courant et de tension, prises sinusoïdales, parcourent la ligne et contribuent à un champ électromagnétique dont la phase respective des grandeurs électriques d'excitation est fonction de la position du doublet infinitésimal le long de l'antenne. La figure 5.6 reprend la forme de l'onde de courant d'excitation le long de l'antenne.
L'interprétation telle qu'envisagée, à savoir l'ouverture d'une ligne parallèle et addition des champs rayonnés par une succession de segments infinitésimaux, conduit à un résultat analytiquement correct. Après calculs, le champ électrique à grande distance vaut
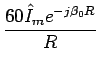 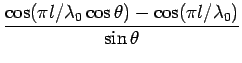 |
(5.45) |
|
L'antenne longue la plus utilisée est l'antenne demi longueur d'onde,
l = ![]() , ce qui correspond à un champ électrique
, ce qui correspond à un champ électrique
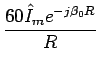 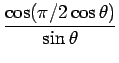 |
(5.46) |
En pratique, l'antenne demi longueur d'onde se réduit à une antenne quart d'onde au-dessus d'un plan de masse conducteur. Pour cette dernière, la résistance de rayonnement vaut
| Rrad = 36, 5 [ |
(5.47) |
Pour obtenir la puissance réellement dissipée par l'antenne, il faudra encore considérer la résistance interne de la force électromotrice d'alimentation et la résistance des conducteurs d'alimentation, car c'est à l'adaptation conjuguée que le transfert de puissance sera maximum.
L'antenne longue seule permet d'assurer une directivité en ![]() .
Par contre, le diagramme de rayonnement est isotrope dans le plan
de la terre. Comme il est souvent nécessaire d'orienter le rayonnement
dans une certaine direction, on recourt à des réseaux d'antennes,
formés d'une série d'antenne longues reliées entre elles avec un courant
d'alimentation déphasé. Ce déphasage (noté
.
Par contre, le diagramme de rayonnement est isotrope dans le plan
de la terre. Comme il est souvent nécessaire d'orienter le rayonnement
dans une certaine direction, on recourt à des réseaux d'antennes,
formés d'une série d'antenne longues reliées entre elles avec un courant
d'alimentation déphasé. Ce déphasage (noté ![]() ) déterminé en
fonction de la longueur inter-antennes et montré à la figure 5.7,
est à l'origine de la modification de l'allure du diagramme de rayonnement
dans le plan de terre.
) déterminé en
fonction de la longueur inter-antennes et montré à la figure 5.7,
est à l'origine de la modification de l'allure du diagramme de rayonnement
dans le plan de terre.
La figure 5.8 montre les diagrammes
de rayonnement dans le plan de terre pour différents rapports
![]() /d.
/d.