5.4.4 Propagation en espace libre: équation de FRIIS

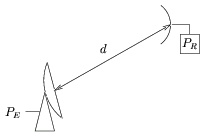
Dans ce paragraphe, on établira la formule de FRIIS donnant l'affaiblissement d'une liaison entre deux antennes séparées par une distance d en espace libre. Cette distance est supposée suffisamment grande pour permettre l'utilisation de l'expression à champ éloigné. De plus, les polarisations sont supposées correspondantes. Les gains des antennes sont notés G_E et G_R (cf. figure 5.15 pour un schéma de principe).

Figure 5.15: Bilan de liaison.

 

La puissance reçue est le produit de l'aire effective de l'antenne par le vecteur de POYNTING incident

$$\left(\vphantom{\frac{P_{E}G_{E}}{4\pi d^{2}}}\right. {\frac{{P_{E}G_{E}}}{{4\pi d^{2}}}} \left.\vphantom{\frac{P_{E}G_{E}}{4\pi d^{2}}}\right) \left(\vphantom{\frac{P_{E}G_{E}}{4\pi d^{2}}}\right. {\frac{{P_{E}G_{E}}}{{4\pi d^{2}}}} \left.\vphantom{\frac{P_{E}G_{E}}{4\pi d^{2}}}\right) \left(\vphantom{\frac{\lambda^{2}}{4\pi}}\right. {\frac{{\lambda^{2}}}{{4\pi}}} \left.\vphantom{\frac{\lambda^{2}}{4\pi}}\right) \left(\vphantom{\frac{\lambda}{4\pi d}}\right. 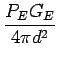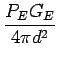{\frac{{\lambda}}{{4\pi d}}} \left.\vphantom{\frac{\lambda}{4\pi d}}\right)^{{2}}_{}$$ (5.68)

On obtient ainsi la formule de FRIIS qui fournit l'affaiblissement en espace libre

$$\epsilon {\frac{{P_{E}}}{{P_{R}}}} \left(\vphantom{\frac{4\pi d}{\lambda}}\right. {\frac{{4\pi d}}{{\lambda}}} \left.\vphantom{\frac{4\pi d}{\lambda}}\right)^{{2}}_{} {\frac{{1}}{{G_{E}G_{R}}}}$$ (5.69)

Le premier facteur de cette expression est appelé l'affaiblissement d'espace; le second exprime tout l'avantage d'antennes directives et montre que les deux antennes jouent à cet égard des rôles identiques. Sous une forme pratique, la formule peut s'écrire en unités logarithmiques -c'est la formule de FRIIS

$$\epsilon$$ (5.70)

On serait tenté de déduire de 5.69 et de 5.70 que les basses fréquences sont avantageuses: cela est vrai pour des antennes de gain donné. Mais il vaut mieux faire ce raisonnement en supposant données les dimensions de l'antenne. En-dessous d'une certaine fréquence, les dimensions de l'antenne sont inférieures à la longueur d'onde et il n'est pas possible d'obtenir de la directivité; les gains de l'antenne restent de l'ordre de 0 [dB], et le raisonnement précédent est correct. Au-dessus de cette fréquence, le rapport dimension/longueur d'onde croît proportionnellement à la fréquence et le gain augmente; la conclusion doit être inversée. En effet, on peut écrire l'affaiblissement fourni par 5.69 sous la forme

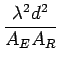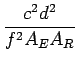$$\epsilon {\frac{{\lambda^{2}d^{2}}}{{A_{E}A_{R}}}} {\frac{{c^{2}d^{2}}}{{f^{2}A_{E}A_{R}}}}$$ (5.71)

L'affaiblissement décroît donc de 20 [dB] par décade, ce qui laisse pressentir l'intérêt des hyperfréquences.