Table des matières of 7.4 Multiplexage par répartition de codes

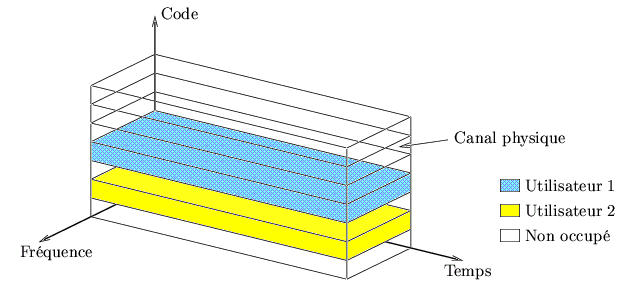
Le principe de base est celui de l'étalement de spectre. Le multiplexage par répartition de codes ne nécessite ni une allocation fixe des fréquences comme en FDM, ni un séquencement strict comme en TDM, comme le montre la figure 7.14.

**Figure:** Multiplexage de ressources par répartition de code (Code Division Multiple Access).

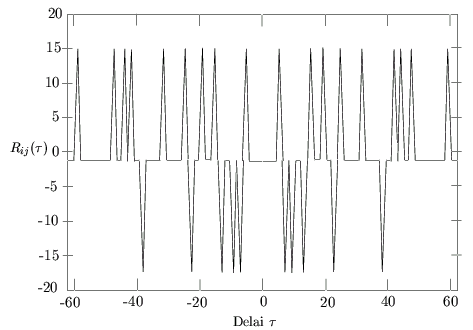
Le facteur limitatif le plus important est celui des intercorrélations entre utilisateurs dès lors que les utilisateurs recourent à des codes distincts. Considérons, pour l'analyse, la situation de la figure 7.15.

**Figure 7.15:** Schéma d'analyse pour l'intercorrélation des séquences étalées.

On prend le cas le plus défavorable de deux utilisateurs i et j parfaitement en phase et travaillant à la même fréquence. On cherche à déterminer l'effet d'interférence dû à l'utilisateur i à la sortie du récepteur j . Soit b_i(t) la séquence (en forme bipolaire -1, + 1 ) de l'utilisateur i . Soit un décalage $\tau$ entre les horloges de référence des deux utilisateurs. On montre aisément que l'interférence de i à l'entrée de l'organe de décision de j vaut

$\displaystyle \left.\vphantom{v_{j}(\tau)}\right.$ v_j( $\displaystyle \tau$ ) $\displaystyle \left.\vphantom{v_{j}(\tau)}\right\vert _{{b_{j}(t)=0}}^{}$	=	$\displaystyle \int_{{0}}^{{T_{b}}}$ b_i(t - $\displaystyle \tau$ )c_j(t)c_i(t - $\displaystyle \tau$ )dt	(7.6)
	=	$\displaystyle \pm$ $\displaystyle \int_{{0}}^{{T_{b}}}$ c_j(t)c_i(t - $\displaystyle \tau$ )dt	(7.7)

$\displaystyle \left.\vphantom{v_{j}(\tau)}\right.$ v_j( $\displaystyle \tau$ ) $\displaystyle \left.\vphantom{v_{j}(\tau)}\right\vert _{{b_{j}(t)=0}}^{}$ = $\displaystyle \pm$ T_b $\displaystyle \Gamma_{{ji}}^{}$ ( $\displaystyle \tau$ )

(7.8)

$\displaystyle \Gamma_{{ji}}^{}$ ( $\displaystyle \tau$ ) = $\displaystyle {\frac{{1}}{{T_{b}}}}$ $\displaystyle \int_{{0}}^{{T_{b}}}$ c_j(t)c_i(t - $\displaystyle \tau$ )dt

(7.9)

Cette moyenne temporelle est appelée fonction d'intercorrélation partielle. Pour avoir une interférence nulle, il faudrait que cette fonction soit nulle pour toute valeur $\tau$ . En général, les séquences à longueur maximale n'ont pas de bonnes propriétés d'intercorrélation partielle comme le montre la figure 7.16; la fonction d'intercorrélation est loin d'être nulle pour toute valeur de $\tau$ .

**Figure:** Fonction d'intercorrélation de deux séquences pseudo-aléatoires de période N = 63 ([6, 1] et [6, 5, 2, 1] ) (d'après [15, page 608]).