Pour la modélisation de la distribution des appels, nous allons partir
d'un processus aléatoire de dénombrement ou de comptage
D(t)
qui détermine pour tout temps t
le nombre d'appels initiés
après t = 0
. Autrement dit, D(t)
compte le nombre d'appels effectués
pendant l'intervalle ]0, t]
. Il s'agit bien évidemment d'un processus
à valeurs entières dont les réalisations se représentent sous la forme
d'une fonction en escaliers. À la figure 8.4,
on constate qu'au temps
t = 8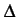 T
, cinq appels ont été initiés.
T
, cinq appels ont été initiés.
Figure 8.4:
Réalisations d'un processus de comptage.
|
|
Plutôt que cette courbe, c'est le nombre d'occurrences pendant tout
intervalle
[t1, t2]
qui nous intéresse; après tout, on devra
bien se choisir une durée typique pour l'analyse. Imaginons que l'on
puisse découper l'axe temporel en intervalles de largeur
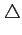 T
tellement étroits qu'ils contiennent tout au plus une
occurrence. Chacun de ces intervalles, référencés par
]n
T
tellement étroits qu'ils contiennent tout au plus une
occurrence. Chacun de ces intervalles, référencés par
]n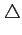 T,(n + 1)
T,(n + 1)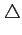 T]
,
est le lieu d'une variable aléatoire binaire Dn
. Dès lors, Dn = 1
implique qu'une tentative d'appel a été menée pendant l'intervalle
de temps
]n
T]
,
est le lieu d'une variable aléatoire binaire Dn
. Dès lors, Dn = 1
implique qu'une tentative d'appel a été menée pendant l'intervalle
de temps
]n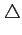 T,(n + 1)
T,(n + 1)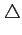 T]
, Dn = 0
mentionne
qu'aucune tentative d'appel n'a été menée pendant cet intervalle.
À supposer que ces variables aléatoires soient indépendantes, la résultante
n'est autre qu'une loi binomiale.
T]
, Dn = 0
mentionne
qu'aucune tentative d'appel n'a été menée pendant cet intervalle.
À supposer que ces variables aléatoires soient indépendantes, la résultante
n'est autre qu'une loi binomiale.
Par généralisation, pour toute constante positive 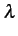 > 0
, il
est possible de choisir une valeur pour
> 0
, il
est possible de choisir une valeur pour
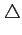 T
telle que
T
telle que
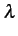
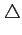 T < 1
(pour pouvoir définir une probabilité). Si
T < 1
(pour pouvoir définir une probabilité). Si
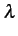
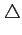 T
représente
la probabilité de réussite8.3 de chacune des variables
D1, D2, ...
, considérant
un intervalle de temps
T = m
T
représente
la probabilité de réussite8.3 de chacune des variables
D1, D2, ...
, considérant
un intervalle de temps
T = m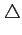 T
, on obtient les probabilités
suivantes:
T
, on obtient les probabilités
suivantes:
- probabilité d'avoir n
tentatives d'appels pendant la durée T
et donc sur les m
intervalles de temps
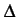 T
(n
réussites
pour la loi binomiale):
T
(n
réussites
pour la loi binomiale):
- probabilité d'avoir m - n
intervalles de temps
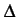 T
sans tentative
d'appel (m - n
échecs)
T
sans tentative
d'appel (m - n
échecs)
Le nombre d'occurrences Dm
obtenues pendant un intervalle de
temps
T = m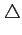 T
obéit dès lors à la fonction de densité de
probabilité suivante (loi binomiale)
T
obéit dès lors à la fonction de densité de
probabilité suivante (loi binomiale)
fDm(n) = p(Dm=n) =   |
(8.10) |
où
Cmn =  . La variable aléatoire Dm
,
représentant le nombre de tentatives d'appel pendant l'intervalle
de temps T
, est une variable aléatoire binomiale de moyenne
m(
. La variable aléatoire Dm
,
représentant le nombre de tentatives d'appel pendant l'intervalle
de temps T
, est une variable aléatoire binomiale de moyenne
m( ) =
) = 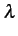 T
.
Le paramètre
T
.
Le paramètre 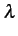 représente donc le nombre moyen de tentatives
d'appels par unité de temps tandis que
représente donc le nombre moyen de tentatives
d'appels par unité de temps tandis que 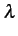 T
représente le
nombre moyen de tentatives d'appels sur l'intervalle de temps
T
.
T
représente le
nombre moyen de tentatives d'appels sur l'intervalle de temps
T
.
Notes
- ... réussite8.3
- Et donc
(1 -
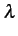
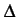 T)
représente l'absence de tentative.
T)
représente l'absence de tentative.
Marc Van Droogenbroeck. Tous droits réservés.
2007-10-27
![]() T
T
![]() T,(n + 1)
T,(n + 1)![]() T]
T]
![]() T,(n + 1)
T,(n + 1)![]() T]
T]
![]() > 0
> 0
![]() T
T
![]()
![]() T < 1
T < 1
![]()
![]() T
T
![]() T
T
![]() T
T
![]()
![]() T)n =
T)n = ![]()
![]()
![]()
![]() T
T
![]()
![]() T)m-n =
T)m-n = ![]() 1 -
1 - ![]()
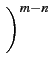
![]() T
T
![]()
![]() ) =
) = ![]() T
T
![]()
![]() T
T
![]()
![]() T)
T)

