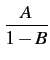lignes du réseau soient occupées) en fonction
de la charge et du nombre de lignes caractérisant le tronçon considéré.
Pour analyser la charge d'un réseau, il faut prendre en compte le
nombre de tentatives d'appel, le nombre de connexions en cours et
le nombre d'arrêts d'appel.
Le nombre de tentatives d'appel peut être vu comme un processus de
dénombrement. Pendant l'intervalle de temps
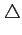 t
(intervalle
de temps d'observation), le nombre de tentatives d'appel NA
est donc une variable aléatoire de POISSON telle que
t
(intervalle
de temps d'observation), le nombre de tentatives d'appel NA
est donc une variable aléatoire de POISSON telle que
p(NA=n) = 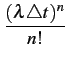 e- e-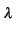 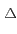 t, n = 0, 1, ... t, n = 0, 1, ... |
(8.35) |
où 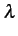 représente le nombre moyen de tentatives par unité de
temps.
représente le nombre moyen de tentatives par unité de
temps.
De même, le nombre d'arrêts ND
pour un nombre d'arrêt moyen
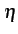 par unité de temps vaut
par unité de temps vaut
p(ND=n) = 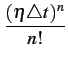 e- e-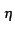 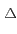 t, n = 0, 1, ... t, n = 0, 1, ... |
(8.36) |
À tout moment, des tentatives d'appel et des arrêts peuvent avoir
lieu sur la ligne; la charge fluctue donc entre 0
et N
appels
en cours. Pour un intervalle de temps très court dt
, la probabilité
d'avoir exactement une tentative d'appel (n = 1
) vaut
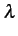 dte-
dte-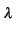 dt
dt 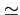
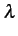 dt
alors que la probabilité d'avoir un appel qui se termine vaut
dt
alors que la probabilité d'avoir un appel qui se termine vaut
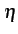 dte-
dte-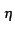 dt
dt 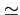
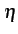 dt
.
dt
.
Dès lors, à supposer que k
lignes sur un total de N
lignes soient
occupées à l'instant t
, on calcule respectivement trois probabilités
sur un intervalle de temps dt
- P1
la probabilité d'une tentative d'appel,
- P2
la probabilité d'un arrêt et
- P3
la probabilité d'un statu quo en matière d'occupation de
lignes.
Elles valent respectivement
P1 = 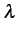 dt dt |
(8.37) |
P2 = Ck1(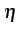 dt)1(1 - dt)1(1 - 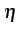 dt)k-1 dt)k-1 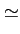 k k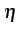 dt dt |
(8.38) |
car on tient compte du fait que n'importe quelle ligne parmi les k
lignes peut se libérer pendant l'intervalle de temps dt
. Finalement,
l'événement de statu quo se produit quand il n'y a pas de tentative
d'appel et qu'aucune des k
lignes occupées n'est sujet à un relâchement.
Ainsi, la probabilité P3
est donnée par
| P3 |
= |
(1 - 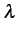 dt)(1 - k dt)(1 - k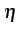 dt) dt) |
(8.39) |
| |
= |
1 - 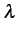 dt - k dt - k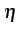 dt + k dt + k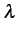 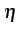 (dt)2 (dt)2 |
(8.40) |
| |
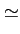 |
1 - 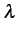 dt - k dt - k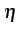 dt dt |
(8.41) |
Définissons alors p(k;t + dt)
comme la probabilité qu'il y ait k
lignes occupées à l'instant t + dt
. Il est alors possible de déterminer
p(k;t + dt)
en utilisant les probabilités
P1, P2
et P3
| p(k;t + dt) |
= |
P3 p(k;t) + P1 p(k - 1;t) + P2 p(k + 1;t) |
(8.42) |
| |
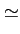 |
(1 - 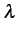 dt - k dt - k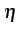 dt) p(k;t) + dt) p(k;t) + 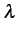 dt p(k - 1;t) + (k + 1) dt p(k - 1;t) + (k + 1)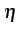 dt p(k + 1;t) dt p(k + 1;t) |
|
Le premier terme correspond au fait qu'il y avait déjà k
lignes
occupées à l'instant t
mais qu'aucune tentative d'appel ni d'arrêt
n'ait eu lieu. Le deuxième terme correspond au fait qu'il y avait
k - 1
lignes occupées à l'instant t
mais qu'une tentative d'appel
(dès lors réussie) ait eu lieu. Enfin, le dernier terme correspond
au fait qu'il y avait k + 1
lignes occupées à l'instant t
et qu'une
ligne se soit libérée pendant l'intervalle de temps dt
. Il existe
cependant deux cas particuliers correspondant à k = 0
et k = N
p(0;t + dt) = (1 - 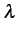 dt) p(0;t) + dt) p(0;t) + 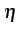 dt p(1;t) dt p(1;t) |
(8.43) |
représentant le cas où aucune ligne n'est occupée (il n'y a donc pas
de possibilité de relâchement d'une ligne) et
p(N;t + dt) = (1 - 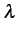 dt - N dt - N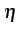 dt) p(N;t) + dt) p(N;t) + 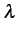 dt p(N - 1;t) dt p(N - 1;t) |
(8.44) |
pour le cas où toutes les lignes sont occupées (une nouvelle
tentative d'appel ne peut donc être générée).
En régime, on peut faire l'hypothèse que les probabilités ne sont
pas fonction du temps et écrire
| p(k;t + dt) = p(k;t) = Pk, k = 0, 1, 2, ..., N |
(8.45) |
L'équation de transition peut alors s'écrire
| |
|
Pk = (1 - 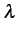 dt - k dt - k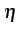 dt) Pk + dt) Pk + 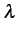 dt Pk-1 + (k + 1) dt Pk-1 + (k + 1)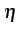 dt Pk+1 dt Pk+1 |
(8.46) |
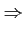 |
|
0 = 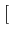 (- (- 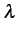 - k - k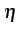 ) Pk + ) Pk + 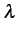 Pk-1 + (k + 1) Pk-1 + (k + 1)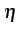 Pk+1 Pk+1![$\displaystyle \left.\vphantom{(-\lambda-k\eta) P_{k}+\lambda P_{k-1}+(k+1)\eta P_{k+1}}\right]$](img982.gif) dt dt |
(8.47) |
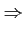 |
|
(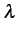 + k + k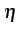 ) Pk = ) Pk = 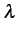 Pk-1 + (k + 1) Pk-1 + (k + 1)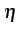 Pk+1, 0 < k < N Pk+1, 0 < k < N |
(8.48) |
De même, les deux cas particuliers deviennent
| |
|
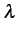 P0 = P0 = 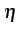 P1, k = 0 P1, k = 0 |
(8.49) |
| |
|
(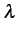 + N + N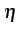 ) PN = ) PN = 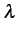 PN-1, k = N PN-1, k = N |
(8.50) |
De plus, les probabilités Pk
doivent respecter la condition
suivante
| P0 + P1 + ... + PN = 1 |
(8.51) |
On peut montrer [21] que l'expression de Pk
vérifiant
toutes ces conditions est donnée par
Pk = 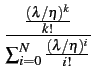 |
(8.52) |
Cette formule représente ainsi la probabilité d'avoir k
lignes occupées. Elle est valable
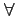 k
k 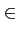 [0, N]
.
[0, N]
.
L'état qui résulte d'une occupation de toutes les lignes est appelé
congestion. Si un appel est rejeté en raison
d'une occupation des N
lignes, la probabilité de cet événement
de blocage est celle de PN
(k = N)
B = PN = 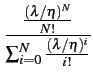 |
(8.53) |
Cette expression de la probabilité de blocage est la formule
dite d'ERLANG B.
Proposition 36
[Espérance de la loi la distribution d'ERLANG
B] L'espérance des probabilités Pk
fournit
le nombre moyen de lignes occupées, c'est-à-dire la charge du trafic
écoulé. Cette espérance vaut
Démonstration. En effet,
E{k} = 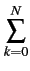 k k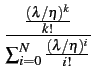 = = 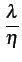 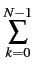 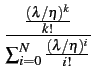 = = 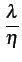 (1 - B) = A(1 - B) (1 - B) = A(1 - B) |
(8.55) |
où A
est la charge offerte du faisceau et A(1 - B)
la charge réelle.
Dans la mesure où la probabilité de blocage est petite, l'occupation
moyenne des N
lignes est égale à
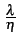 .
.
La probabilité de blocage s'exprime donc par l'expression
B = PN = 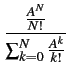 , A = , A = 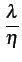 |
(8.56) |
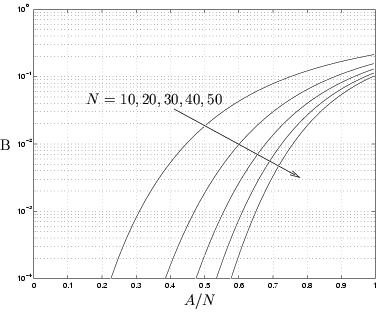
La probabilité de blocage augmente avec la charge A
et décroît
avec N
, comme le montre graphiquement la figure 8.6.
Pour une probabilité de blocage fixée, le rapport A/N
(charge offerte
à chaque utilisateur) est proportionnel au nombre de lignes N
.
Dès lors, la charge A
, pour une probabilité de blocage fixée, augmente
plus que proportionnellement en fonction du nombre de lignes N
.
Pour s'en convaincre, il suffit de regarder le tableau .
Doubler la valeur de N
de 10 à 20 entraîne la multiplication de
A
par
12/4, 5 = 2, 67
. Pour B = 1%
, on observe un gain important
en efficacité lorsque l'on passe de 10 à 20 lignes tandis que ce gain
est nettement moins important lorsque l'on doit, pour une même probabilité
de blocage, ajouter des lignes à un faisceau contenant déjà 50 à 60
lignes.
Figure 8.6:
Loi de probabilité ERLANG B (d'après [21, page 271]).
|
|
Tableau 8.1:
Illustration des proportions pour B = 0, 01
| N
|
10 |
20 |
30 |
40 |
50 |
60 |
70 |
80 |
90 |
100 |
| A
|
4,5 |
12,0 |
20,3 |
29,0 |
37,9 |
46,9 |
56,1 |
65,4 |
74,7 |
84,1 |
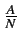
|
0,45 |
0,60 |
0,68 |
0,73 |
0,76 |
0,78 |
0,80 |
0,82 |
0,83 |
0,84 |
|
Le dimensionnement d'un faisceau téléphonique
est réalisé en recherchant la charge maximale A
(en ERLANG)
qui peut être fournie lorsque désire maintenir la probabilité de blocage
B
en-dessous d'un certain seuil, par exemple B = 0, 01
ou 0, 02
,
qui est une valeur typique pour le dimensionnement d'un faisceau dans
un réseau. La formule d'ERLANG B est souvent utilisée dans
ce but parce qu'elle est tabulée et facilement interprétable, bien
qu'elle fournisse une valeur plus faible pour B
que certaines formules
établies à partir d'hypothèses autres quant au trafic. En effet, la
formule d'ERLANG B ne tient pas compte du fait qu'une tentative
d'appel ayant échoué peut être reconduite jusqu'à acceptation par
le réseau.
Insistons sur le fait que la charge maximale ne représente pas la
charge moyenne offerte à chaque utilisateur, mais une charge globale
maximale.
Une table de la loi d'ERLANG B est donnée
à la page ![[*]](crossref.gif) . Soit, par exemple, N = 20
et B = 0, 01
. À partir de la table, nous obtenons
A = 12, 0 [E]
.
Si une charge
A0 = 0, 03 [E]
doit être offerte à chaque utilisateur
en moyenne, le nombre d'utilisateurs doit être limité à
M = A/A0 = 400
.
. Soit, par exemple, N = 20
et B = 0, 01
. À partir de la table, nous obtenons
A = 12, 0 [E]
.
Si une charge
A0 = 0, 03 [E]
doit être offerte à chaque utilisateur
en moyenne, le nombre d'utilisateurs doit être limité à
M = A/A0 = 400
.
L'effet d'une tentative d'appel ayant échoué mais reconduite jusqu'à
obtention d'une ligne peut être modélisé assez facilement. Appelons
A'
la charge réelle qui tient compte de la reconduite des tentatives
échouées. On a
A' = A + AB + (AB)B + (AB2)B + ... = 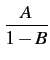 |
(8.57) |
La table de la figure 8.2 peut être utilisée
pour trouver A'
. Il est important de noter qu'en principe le réseau
doit être dimensionné pour cette charge A'
et non pour la charge
A
. Alors A
peut être obtenue par A = (1 - B)A'
. Par exemple,
pour B = 0, 02
et N = 30
, la table donne A = 21, 9
qui doit être
vu comme la valeur de A'
. La valeur de A
est alors égale à
(1 - 0, 02) x 21, 9 = 21, 5
.
Si on désire offrir à chaque utilisateur une charge moyenne
A0 = 0, 03
,
on doit limiter le nombre d'utilisateurs à
M = A/A0 = 715
, contre
730
lorsque qu'aucune tentative ayant échoué n'est reconduite.
Tableau 8.2:
Tables de la loi d'ERLANG B.
| |
B
|
|
B
|
| N
|
0,01 |
0,005 |
0,003 |
0,001 |
N
|
0,01 |
0,005 |
0,003 |
0,001 |
| 1 |
0,01 |
0,005 |
0,003 |
0,001 |
31 |
21,2 |
19,9 |
19,0 |
17,4 |
| 2 |
0,153 |
0,105 |
0,081 |
0,046 |
32 |
22,0 |
20,7 |
19,8 |
18,2 |
| 3 |
0,46 |
0,35 |
0,29 |
0,19 |
33 |
22,9 |
21,5 |
20,6 |
19,0 |
| 4 |
0,87 |
0,7 |
0,6 |
0,44 |
34 |
23,8 |
22,3 |
21,4 |
19,7 |
| 5 |
1,4 |
1,1 |
1,0 |
0,8 |
35 |
24,6 |
23,2 |
22,2 |
20,5 |
| 6 |
1,9 |
1,6 |
1,4 |
1,1 |
36 |
25,5 |
24,0 |
23,1 |
21,3 |
| 7 |
2,5 |
2,2 |
1,9 |
1,6 |
37 |
26,4 |
24,8 |
23,9 |
22,1 |
| 8 |
3,1 |
2,7 |
2,5 |
2,1 |
38 |
27,3 |
25,7 |
24,7 |
22,9 |
| 9 |
3,8 |
3,3 |
3,1 |
2,6 |
39 |
28,1 |
26,5 |
25,5 |
23,7 |
| 10 |
4,5 |
4,0 |
3,6 |
3,1 |
40 |
29,0 |
27,4 |
26,3 |
24,4 |
| 11 |
5,2 |
4,6 |
4,3 |
3,7 |
41 |
29,9 |
28,2 |
27,2 |
25,2 |
| 12 |
5,9 |
5,3 |
4,9 |
4,2 |
42 |
30,8 |
29,1 |
28,0 |
26,0 |
| 13 |
6,6 |
6,0 |
5,6 |
4,8 |
43 |
31,7 |
29,9 |
28,8 |
26,8 |
| 14 |
7,4 |
6,7 |
6,2 |
5,4 |
44 |
32,5 |
30,8 |
29,7 |
27,6 |
| 15 |
8,1 |
7,4 |
6,9 |
6,1 |
45 |
33,4 |
31,7 |
30,5 |
28,4 |
| 16 |
8,9 |
8,1 |
7,6 |
6,7 |
46 |
34,3 |
32,5 |
31,4 |
29,3 |
| 17 |
9,7 |
8,8 |
8,3 |
7,4 |
47 |
35,2 |
33,4 |
32,2 |
30,1 |
| 18 |
10,4 |
9,6 |
9,0 |
8,0 |
48 |
36,1 |
34,2 |
33,1 |
30,9 |
| 19 |
11,2 |
10,3 |
9,8 |
8,7 |
49 |
37,0 |
35,1 |
33,9 |
31,7 |
| 20 |
12,0 |
11,1 |
10,5 |
9,4 |
50 |
37,9 |
36,0 |
34,8 |
32,5 |
| 21 |
12,8 |
11,9 |
11,2 |
10,1 |
51 |
38,8 |
36,9 |
35,6 |
33,3 |
| 22 |
13,7 |
12,6 |
12,0 |
10,8 |
52 |
39,7 |
37,7 |
36,5 |
34,2 |
| 23 |
14,5 |
13,4 |
12,7 |
11,5 |
53 |
40,6 |
38,6 |
37,3 |
35,0 |
| 24 |
15,3 |
14,2 |
13,5 |
12,2 |
54 |
41,5 |
39,5 |
38,2 |
35,8 |
| 25 |
16,1 |
15,0 |
14,3 |
13,0 |
55 |
42,4 |
40,4 |
39,0 |
36,6 |
| 26 |
17,0 |
15,8 |
15,1 |
13,7 |
56 |
43,3 |
41,2 |
39,9 |
37,5 |
| 27 |
17,8 |
16,6 |
15,8 |
14,4 |
57 |
44,2 |
42,1 |
40,8 |
38,3 |
| 28 |
18,6 |
17,4 |
16,6 |
15,2 |
58 |
45,1 |
43,0 |
41,6 |
39,1 |
| 29 |
19,5 |
18,2 |
17,4 |
15,9 |
59 |
46,0 |
43,9 |
42,5 |
40,0 |
| 30 |
20,3 |
19,0 |
18,2 |
16,7 |
60 |
47,0 |
44,8 |
43,4 |
40,8 |
|
Marc Van Droogenbroeck. Tous droits réservés.
2007-10-27
![]() t
t
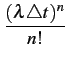 e-
e-![]()
![]() t, n = 0, 1, ...
t, n = 0, 1, ...![]()
![]()
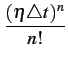 e-
e-![]()
![]() t, n = 0, 1, ...
t, n = 0, 1, ...![]() dte-
dte-![]() dt
dt ![]()
![]() dt
dt
![]() dte-
dte-![]() dt
dt ![]()
![]() dt
dt
![]() dt
dt![]() dt)1(1 -
dt)1(1 - ![]() dt)k-1
dt)k-1 ![]() k
k![]() dt
dt![]() dt)(1 - k
dt)(1 - k![]() dt)
dt)![]() dt - k
dt - k![]() dt + k
dt + k![]()
![]() (dt)2
(dt)2![]()
![]() dt - k
dt - k![]() dt
dt![]()
![]() dt - k
dt - k![]() dt) p(k;t) +
dt) p(k;t) + ![]() dt p(k - 1;t) + (k + 1)
dt p(k - 1;t) + (k + 1)![]() dt p(k + 1;t)
dt p(k + 1;t)![]() dt) p(0;t) +
dt) p(0;t) + ![]() dt p(1;t)
dt p(1;t)![]() dt - N
dt - N![]() dt) p(N;t) +
dt) p(N;t) + ![]() dt p(N - 1;t)
dt p(N - 1;t)![]() dt - k
dt - k![]() dt) Pk +
dt) Pk + ![]() dt Pk-1 + (k + 1)
dt Pk-1 + (k + 1)![]() dt Pk+1
dt Pk+1![]()
![]() (-
(- ![]() - k
- k![]() ) Pk +
) Pk + ![]() Pk-1 + (k + 1)
Pk-1 + (k + 1)![]() Pk+1
Pk+1![]() dt
dt![]()
![]() + k
+ k![]() ) Pk =
) Pk = ![]() Pk-1 + (k + 1)
Pk-1 + (k + 1)![]() Pk+1, 0 < k < N
Pk+1, 0 < k < N![]() P0 =
P0 = ![]() P1, k = 0
P1, k = 0![]() + N
+ N![]() ) PN =
) PN = ![]() PN-1, k = N
PN-1, k = N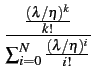
![]() k
k ![]() [0, N]
[0, N]
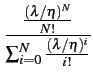
![]() k
k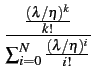 =
= ![]()
![]()
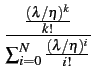 =
= ![]() (1 - B) = A(1 - B)
(1 - B) = A(1 - B)![]()
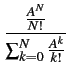 , A =
, A = ![]()
![]()
![[*]](crossref.gif) . Soit, par exemple, N = 20
. Soit, par exemple, N = 20