est liée au signal sous-jacent par la relation
xs(t) = 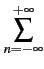 x[nTs] x[nTs]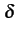 (t - nTs) (t - nTs) |
(1.14) |
La transformée de FOURIER de ce signal vaut
 s(f ) s(f ) |
= |
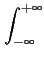 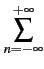 x[nTs] x[nTs]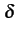 (t - nTs)e-2 (t - nTs)e-2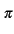 jftdt jftdt |
(1.15) |
| |
= |
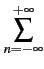 x[nTs] x[nTs]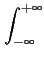 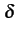 (t - nTs)e-2 (t - nTs)e-2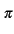 jftdt jftdt |
(1.16) |
| |
= |
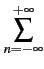 x[nTs]e-2 x[nTs]e-2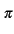 jfnTs jfnTs |
(1.17) |
On remarquera que cette fonction est continue et périodique de période
fs = 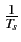 ; la connaissance de cette fonction sur l'intervalle
[0, fs[
suffit donc. En effet,
; la connaissance de cette fonction sur l'intervalle
[0, fs[
suffit donc. En effet,
 (f + fs) = (f + fs) = 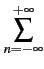 x[nTs]e-2 x[nTs]e-2 j(f+fs)nTs = j(f+fs)nTs = 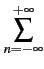 x[nTs]e-2 x[nTs]e-2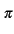 jfnTse-2 jfnTse-2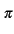 jn = jn =  (f ) (f ) |
(1.18) |
Ce phénomène est bien connu: l'échantillonnage dans le domaine temporel
entraîne l'apparition de copies de la transformée au droit des fréquences
multiples de fs
. Il est d'usage de définir une fréquence
normalisée ou fréquence
réduite F
par
F = 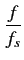 |
(1.19) |
de sorte que F
parcourt l'intervalle [0, 1[
ou
[- 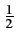 ,
,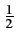 [
.
Si en plus de l'utilisation de la fréquence normalisée, on adopte
l'écriture x[n]
en lieu et place de x[nTs]
, la transformée
de FOURIER à temps discret s'exprime sous la forme normalisée
suivante.
[
.
Si en plus de l'utilisation de la fréquence normalisée, on adopte
l'écriture x[n]
en lieu et place de x[nTs]
, la transformée
de FOURIER à temps discret s'exprime sous la forme normalisée
suivante.
Définition 2
[Transformée de FOURIER à temps
discret normalisée]
On déduit la formule inverse
ou
On montre [5, page 45] que si la séquence x[n]
est de module sommable, c'est-à-dire si
la transformée converge uniformément vers une fonction continue de
F
.
Si, par contre, x[n]
est de carré sommable, à savoir
sans être de module sommable, alors la série converge en moyenne quadratique.
Il peut ne pas y avoir convergence uniforme. La fonction
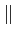
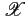 (f )
(f )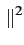 est désignée par le terme de spectre. Dans
la littérature, ce terme est aussi associé à la fonction
est désignée par le terme de spectre. Dans
la littérature, ce terme est aussi associé à la fonction
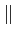
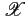 (f )
(f )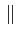 .
Les deux expressions deviennent équivalentes si l'on utilise l'échelle
logarithmique des décibels.
.
Les deux expressions deviennent équivalentes si l'on utilise l'échelle
logarithmique des décibels.
Exemple. Transformée de FOURIER
d'un signal rectangulaire.
Considérons une fonction rectangulaire
rectN[n]
valant
1
pour
n 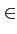 { - N, ..., N}
et 0
ailleurs. On calcule
alors
{ - N, ..., N}
et 0
ailleurs. On calcule
alors
 (F) (F) |
= |
 x[n]e-2 x[n]e-2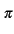 jFn jFn |
(1.25) |
| |
= |
e2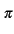 jFN(1 +...+ e-2 jFN(1 +...+ e-2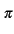 jF(2N+1)) jF(2N+1)) |
(1.26) |
| |
= |
e2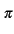 jFN jFN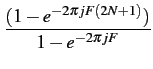 |
(1.27) |
| |
= |
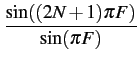 |
(1.28) |
Ce signal est purement réel; il est représenté à la figure 1.1
pour deux valeurs de N
.
Figure 1.1:
Transformées de FOURIER d'un signal rectangulaire (N = 2
et
N = 5
).
|
|
La transformée inverse a pour expression
La fonction complexe
 (F)
peut aussi s'exprimer
sous la forme
(F)
peut aussi s'exprimer
sous la forme
dont le terme d'amplitude est appelé spectre d'amplitude
de x[n].
Exemple. Impulsion de DIRAC
discrète décalée.
Considérons le signal
 (F) = e2 (F) = e2 jF jF |
(1.32) |
Tout comme dans le cas d'une fonction continue, l'énergie du signal
est conservée par rapport à sa transformée de FOURIER.
Définition 3
L'énergie totale du signal vaut
Proposition 4
L'égalité de PARSEVAL s'exprime
sous la forme
Le cas des séquences périodiques est particulier car cette périodicité
résulte généralement d'une opération d'échantillonnage; il s'agit
alors d'une périodicité fictive.
Définition 5
Une séquence est périodique s'il existe une valeur
entière N
telle que
pour toute valeur n
.
Marc Van Droogenbroeck. Tous droits réservés.
2007-10-27
![]()
![]() (f + fs) =
(f + fs) = ![]() x[nTs]e-2
x[nTs]e-2![]() j(f+fs)nTs =
j(f+fs)nTs = ![]() x[nTs]e-2
x[nTs]e-2![]() jfnTse-2
jfnTse-2![]() jn =
jn = ![]() (f )
(f )![]()
![]() ,
,![]() [
[
![]() (F) =
(F) = ![]() x[n]e-2
x[n]e-2![]() jFn
jFn![]()
![]() (F)e2
(F)e2![]() jFndF
jFndF![]()
![]() (F)e2
(F)e2![]() jFndF
jFndF![]()
![]() x[n]
x[n]![]() < +
< + ![]()
![]()
![]() (f )
(f )![]()
![]()
![]() (f )
(f )![]()
![]() { - N, ..., N}
{ - N, ..., N}
![]() (F)
(F)![]() x[n]e-2
x[n]e-2![]() jFn
jFn![]() jFN(1 +...+ e-2
jFN(1 +...+ e-2![]() jF(2N+1))
jF(2N+1))![]() jFN
jFN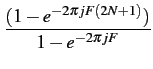
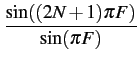
![]()
![]() (F)e2
(F)e2![]() jFndF
jFndF![]() (F)
(F)
![]() (F) =
(F) = ![]()
![]() (F)
(F)![]() ej
ej![]() (F)
(F)![]()
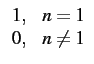 =
= ![]() [n - 1]
[n - 1]![]() (F) = e2
(F) = e2![]() jF
jF![]()
![]() x[n]
x[n]![]()
![\includegraphics[width=14cm]{matlab/tdftRectangle}](img105.gif)