1.2.4 Observation spectrale

L'estimation spectrale s'articule sur la notion de transformée de FOURIER. Dès lors, la compréhension de ses propriétés est essentielle. Pour toute transformée de FOURIER, on distingue les deux critères de qualité suivants: précision sur la position des raies et résolution.

1.2.4.1 Précision

Pour illustrer l'utilisation de la transformée de FOURIER discrète dans l'observation de spectres de signaux, considérons la suite x[n] obtenue par échantillonnage de l'exponentielle complexe e^2$\pi$jF₀t à la cadence F_s = 1/T_s (cet exemple est tiré de [5]). En posant f₀ = F₀/F_s < 1 , on a x[n] = e^2$\pi$jf₀n . Le fait de réduire la durée d'observation à un intervalle N fait apparaître des ondulations dans la transformée de FOURIER à temps discret du signal. Ce phénomène est illustré à la figure 1.2 pour N = 32 et f₀ = ${\frac{{7}}{{32}}}$ .

Figure 1.2: Transformée de FOURIER à temps discret de l'exponentielle complexe f₀ = ${\frac{{7}}{{32}}}$ avec N = 32.

Comme la transformée de FOURIER discrète correspond à l'échantillonnage à la transformée à temps discret aux points de fréquence k/N , elle est en général constituée de valeurs différentes de 0 , sauf si f₀ est exactement un multiple de 1/N . Ces deux situations sont représentées respectivement à la figure 1.3 et 1.4.

Figure 1.3: Transformée de FOURIER discrète de l'exponentielle complexe f₀ = ${\frac{{7}}{{32}}}$ avec N = 32.

Figure 1.4: Transformée de FOURIER discrète de l'exponentielle complexe f₀ = 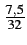${\frac{{7,5}}{{32}}}$ avec N = 32.

Comme on peut le voir à la figure 1.4, une exponentielle dont la fréquence n'est pas un multiple de 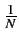${\frac{{1}}{{N}}}$ apparaît sous la forme de plusieurs raies parmi lesquelles la plus proche est celle dont l'amplitude est maximale.

1.2.4.2 Résolution en fréquence

La précision ne doit pas être confondue avec la résolution qui est le pouvoir de distinguer deux fréquences voisines dans un signal. Il est commode de définir la résolution par l'écart minimum en fréquence qu'il faut mettre entre deux sinusoïdes d'amplitudes différentes pour observer sur le spectre de leur somme un creux de plus de 3 [dB] entre les deux maxima.

Figure 1.5: Résolution en fréquence.

 

Comme on l'a vu, le fait d'avoir limité le nombre de valeurs traitées à N conduit à l'apparition de lobes dans le spectre d'une sinusoïde. Le lobe principal a une largeur égale à 2/N . Il s'ensuit que, si x[n] contient deux sinusoïdes dont les fréquences sont séparées de moins de 1/N , les lobes principaux de chacune d'elles seront si proches qu'il sera difficile de les distinguer avec certitude. Et ceci est d'autant plus vrai que les deux amplitudes sont très différentes. Ainsi, si f_s = 1/T_s désigne la fréquence d'échantillonnage, la résolution R exprimée en [Hz] est de l'ordre de grandeur de f_s/N qui est précisément l'inverse du temps total d'analyse, à savoir T = NT_s .

Proposition 8   La résolution en fréquence est de l'ordre de grandeur de l'inverse du temps total d'analyse.

Le produit R x T joue en quelque sorte le rôle de facteur de mérite dans l'utilisation de la transformée de FOURIER à temps discret pour la recherche de fréquences. Typiquement, si on choisit R et T tels que le produit R x T 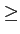$\geq$ 3 , les fréquences seront faciles à séparer.

1.2.4.3 Spectre à court terme

Comme l'analyse en fréquence classique est une opération qui couvre la totalité de l'axe des fréquences, cette opération effectue une moyenne sur l'axe des temps. Cet effet moyenneur peut aller jusqu'à occulter les phénomènes à observer. Cela ne signifie pas que l'information soit détruite. La transformée de FOURIER est en effet bijective sous les conditions d'existence énoncées précédemment.

Prenons l'exemple d'une onde continue x(t) constituée de deux portions successives de fréquences f₁ et f₂ (cf. figure 1.6).

Figure 1.6: Deux portions de sinusoïdes et le spectre correspondant (d'après [5]).

Sa transformée de FOURIER contient l'information concernant l'ordre dans lequel apparaissent les sinusoïdes. Toutefois cette information n'est pas explicite, même si elle se trouve dans l'information de phase. Par conséquent, l'observation du seul module nous fait échapper l'apparition de f₁ avant f₂ .

Par contre, si on découpe le segment de données en N_si sous-intervalles consécutifs pour lesquels on calcule la transformée de FOURIER, le spectre montre que temporellement la fréquence 0, 1 apparaît avant la fréquence 0, 2 . La figure 1.7 montre les transformées des sous-intervalles successifs.

Figure 1.7: Deux portions de sinusoïdes et le spectre correspondant dans une fenêtre d'analyse glissante (d'après [5]).

En posant N_i le nombre de points dans un intervalle, on peut faire les remarques suivantes:

• la transformée de FOURIER effectue une moyenne sur N_i valeurs: prendre une grande valeur provoque un fort lissage des fluctuations temporelles du signal. Cela implique que les transitions sont moins bien localisées. L'aptitude à séparer deux événements temporels est de l'ordre de N_i ;
• par contre, dans les mêmes conditions, comme chaque transformée de FOURIER discrète dispose de plus de points de calcul, la largeur des lobes (de l'ordre de 1/N_i ) diminue et les pics de fréquence apparaissent plus nettement.

On peut résumer ces remarques en formulant que, lors de l'utilisation de la transformée de FOURIER discrète à court terme, l'amélioration de la résolution temporelle détériore la résolution fréquentielle.