Sous-sections
Considérons une source pouvant émettre deux symboles s0
et s1
avec les probabilités respectives p0
et p1
. Celle-ci peut
dès lors être vue comme une variable aléatoire discrète. Nous considérons
la source sans mémoire, c'est-à-dire que le symbole émis à un certain
temps est indépendant des symboles émis précédemment.
Supposons que la source émette un symbole. Si une des deux probabilités
est unitaire, il n'y a pas de surprise à la sortie et donc aucune
information (on connaît le symbole qui va être émis). Dans le cas
où l'émission des symboles est équiprobable (
p0 = p1 = 0, 5
),
une grande incertitude subsiste sur le symbole émis et la réception
du symbole émis apporte beaucoup d'information. On peut ainsi caractériser
l'information par la probabilité d'émission des symboles.
Définition 39
[Information d'un symbole] Dès
lors, le gain en information apporté par l'observation de l'événement
S = sk
, de probabilité pk
est donné par l'information
de symbole telle que définie par
i(sk) = log2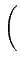 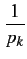  = - log2pk = - log2pk |
(9.92) |
L'information est nulle quand pk
vaut 1
-ce que l'on peut
interpréter comme le fait que la réalisation d'un événement certain
n'apporte aucune information- et elle augmente à mesure que pk
diminue. Cette grandeur s'exprime en bit d'information.
Il convient de ne pas confondre le bit et le bit
d'information qui représentent respectivement
les mesures du débit et du débit d'information. Ainsi, il est tout
à fait possible d'avoir un nombre de bits d'information qui ne soit
pas un nombre entier. En pratique, on ne retrouve guère cette nuance
puisque le terme bit est utilisé pour les deux notions. Il
faudra donc recourir au contexte pour rétablir la distinction.
Soit une source S
comprenant K
symboles. On cherche à caractériser
l'information moyenne fournie par chaque symbole émis.
Définition 40
Cette grandeur est appelée entropie de la source
et notée H(S)
. Dès lors,
Dans le cas d'une source binaire, on peut considérer deux cas particuliers:
- le cas où tous les symboles sont équiprobables. On montre alors que
H(S) = 1
, ce qui implique que l'information apportée lors de l'observation
du symbole vaut un bit.
- le cas où une probabilité pk
vaut 1
. Alors H(S) = 0
; l'information
apportée lors de l'observation du symbole est nulle car on sait a
priori quel symbole va être émis par la source.
Marc Van Droogenbroeck. Tous droits réservés.
2007-10-27
![]()
![]()
![]() = - log2pk
= - log2pk![]() pklog2
pklog2![]()
![]()
![]()