Sous-sections
10.2.4 Masquage
Le masquage provient de la présence d'obstacles. En première approximation,
on peut considérer qu'un obstacle absorbe un certain pourcentage de
la puissance. Ainsi, la puissance transmise ou diffractée ne représente
qu'un certain pourcentage de la puissance incidente. De même, la présence
d'une vitre se traduit par une certaine diminution de puissance.
Pour modéliser les effets de masquage (shadowing
en anglais), aussi appelé évanouissement lent,
nous partons de l'hypothèse suivante. Supposons que toutes les contributions
de masquage à l'affaiblissement A
, en terme de puissance, soient
dues à des facteurs multiplicatifs
A1, A2, ..., AN
,
tous inférieurs à 1
, tels que
| A = A1 x A2 x...x AN |
(10.4) |
représente l'affaiblissement de masquage10.4.
Dès lors qu'il y a masquage, la puissance reçue PR
vaut
| PR = (PE x APL) x A1 x A2 x...x AN |
(10.5) |
où APL
est l'affaiblissement de parcours.
En décibels, l'atténuation totale vaut
| Ltotale = LPL + L = LPL + L1 + L2 +...+ LN |
(10.6) |
Plus spécifiquement, l'atténuation de masquage L
est la somme des
N
contributions
| L = L1 + L2 +...+ LN |
(10.7) |
Si toutes les contributions sont des variables aléatoires de mêmes
espérance et variance, L
est une variable aléatoire normale par
application du théorème de la limite centrale:
L [dB] = L50% [dB] +  [dB] x N(0, 1) = N(L50%, [dB] x N(0, 1) = N(L50%, 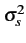 ) [dB] ) [dB] |
(10.8) |
tel que L50%
est la valeur médiane de l'atténuation et
 [dB]
sa variance.
[dB]
sa variance.
En unités naturelles et en écrivant N(0, 1) = X
, l'affaiblissement
vaut
| L |
= |
10L[dB]/10 = 10(L50% [dB]+ [dB] x X)/10 [dB] x X)/10 |
(10.9) |
| |
= |
10L50% [dB]/10 10 [dB] x X/10 = LoV [dB] x X/10 = LoV |
(10.10) |
où
Lo = 10L50% [dB]/10
et
V = 10 [dB] x X/10 [dB] x X/10 |
(10.11) |
est une loi log-normale.
Pour calculer la densité de probabilité de la log-normale, on part
de l'expression de la gaussienne. Soit X
une variable aléatoire
gaussienne centrée, de variance unitaire. Sa densité de probabilité
vaut, pour
x 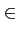 [-
[- 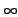 , +
, + 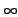 ]
,
]
,
fX(x) = 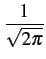 e- e-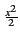 |
(10.12) |
On définit ensuite la variable aléatoire log-normale V
de la manière
suivante
où
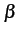 = = 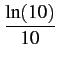 = 0, 23 = 0, 23 |
(10.14) |
La fonction de répartition de V
vaut [21, page 152]
| FV(v) |
= |
p(V 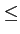 v) = p(e v) = p(e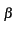  X X 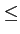 v) = p(X v) = p(X 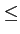 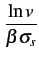 ) ) |
(10.15) |
| |
= |
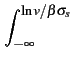 fX(x)dx = fX(x)dx = 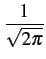 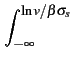 e- e-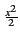 dx dx |
(10.16) |
Par dérivation, il en résulte une densité de probabilité
| fV(v) |
= |
 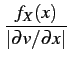 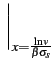 = =  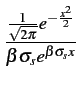 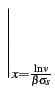 |
(10.17) |
| |
= |
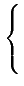 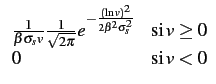 |
(10.18) |
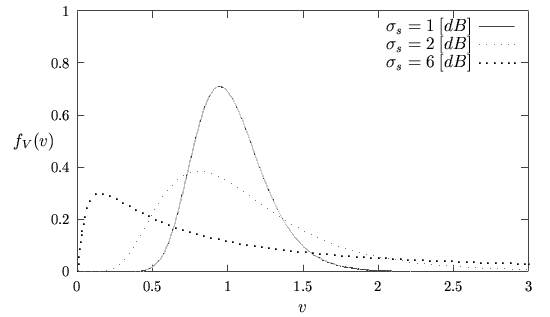
Cette densité de probabilité est représentée à la figure 10.4.
Figure 10.4:
Densité de probabilité d'une loi log-normale.
|
|
La valeur médiane de V
, v50%
, est tirée de la valeur médiane
de X
par
v50% = ex50% = 100 = 1
quelle que soit la valeur
de
 .
.
En pratique, tous les termes ne contribuent pas de la même manière
à l'affaiblissement. D'autre part, on peut montrer que les termes
de diffraction n'obéissent pas à une simple loi additive, en raison
d'une dépendance entre certains termes. Néanmoins, diverses mesures
montrent que la loi log-normale est généralement suffisante pour modéliser
le masquage.
En présence d'un effet de masquage, l'affaiblissement L
est une
variable aléatoire normale
N(L50%, 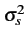 )
(cf. équation 10.8):
)
(cf. équation 10.8):
L [dB] = N(L50%, 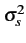 ) [dB] ) [dB] |
(10.19) |
On peut en déduire une variable aléatoire normale centrée Ls
au moyen de l'expression
| L [dB] = L50% [dB] + Ls [dB] |
(10.20) |
où
- L50%
est la valeur médiane10.5 de l'affaiblissement de parcours telle que fournie par les modèles
empiriques résultant de mesures. En effet, ces mesures fournissent
une valeur médiane qui, outre l'affaiblissement de parcours, englobe
un effet moyen de masquage. C'est la raison pour laquelle on classe
les modèles empiriques en fonction de la densité de l'environnement
urbain.
- Ls
, la variable aléatoire de masquage; c'est-à-dire une variable
aléatoire gaussienne de moyenne nulle et d'écart-type
 .
.
La densité de probabilité de Ls
est donc
f (ls) = 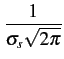 e e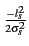 |
(10.21) |
Pour des raisons d'efficacité, il est nécessaire de garantir un niveau
de puissance supérieur à la valeur médiane; l'ingénieur de réseau
n'a guère le choix que d'ajouter une marge supplémentaire de puissance
à l'émission afin d'augmenter la couverture. À
l'ajout de cette marge de
ms [dB]
correspond une probabilité
de couverture supérieure à celle de la puissance médiane pour une
même sensibilité de récepteur. Cette probabilité se calcule par
| p(ls < ms) |
= |
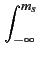 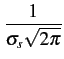 e e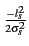 dls dls |
(10.22) |
| |
= |
 + + 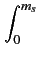 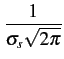 e e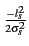 dls dls |
(10.23) |
| |
= |
 + +  erf erf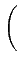 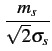 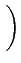 |
(10.24) |
erf(x)
est la fonction d'erreur
erf(x) = 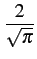 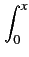 e-t2dt e-t2dt |
(10.25) |
L'effet de masque représente une variation sur les conditions de propagation,
tantôt favorable (par exemple visibilité directe), tantôt défavorable
(par exemple lors de la présence d'un obstacle important entre l'émetteur
et le récepteur). En environnement urbain, l'écart type de la loi
a une valeur typique de 6 [dB]
(d'après [19]).
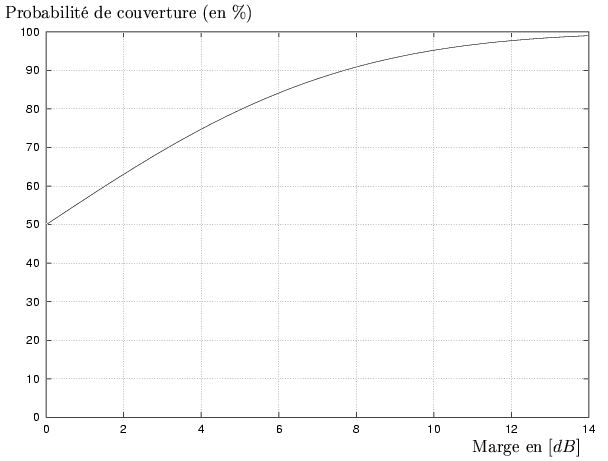
La figure 10.5 montre la probabilité de
couverture (en %) en fonction de la marge additionnelle de puissance.
Figure 10.5:
Pourcentage de couverture tel que défini par un seuil de puissance.
|
|
Notes
- ... masquage10.4
- Cette définition, courante dans la littérature scientifique, peut
prêter à confusion. En effet, en toute rigueur A
représente l'inverse
de l'affaiblissement. Par la suite, nous adopterons néanmoins la définition 10.4.
- ...médiane10.5
- La valeur médiane d'une variable aléatoire normale est théoriquement
égale à sa moyenne. Pour les mesures, le recours à la médiane
est préférable si l'on ne dispose pas d'un large ensemble de réalisations
car elle élimine l'impact des valeurs aberrantes.
Marc Van Droogenbroeck. Tous droits réservés.
2007-10-27
![]() [dB]
[dB]
![]() [dB] x X)/10
[dB] x X)/10![]() [dB] x X/10 = LoV
[dB] x X/10 = LoV![]() [dB] x X/10
[dB] x X/10![]() [-
[- ![]() , +
, + ![]() ]
]
![]() e-
e-![]()
![]() = e
= e![]()
![]() X
X![]() =
= 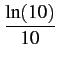 = 0, 23
= 0, 23![]() v) = p(e
v) = p(e![]()
![]() X
X ![]() v) = p(X
v) = p(X ![]()
![]() )
)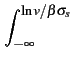 fX(x)dx =
fX(x)dx = ![]()
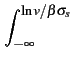 e-
e-![]() dx
dx![]()
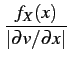
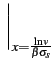 =
= ![]()
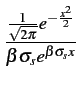
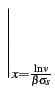
![]()
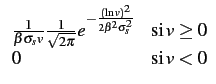
![]()
![]() )
)
![]() ) [dB]
) [dB]![]()
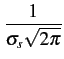 e
e![]()
![]()
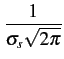 e
e![]() dls
dls![]() +
+ ![]()
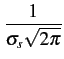 e
e![]() dls
dls![]() +
+ ![]() erf
erf![]()
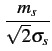
![]()
![]()
![]() e-t2dt
e-t2dt