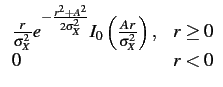Sous-sections
Pour obtenir la statistique qui décrit le phénomène d'évanouissement,
il faut distinguer deux cas, suivant qu'il y ait ou non visibilité
directe -ou du moins, un trajet nettement moins atténué que les autres-
entre l'antenne de la station de base et l'antenne du mobile.
Considérons une série de trajets dus à la diffraction et à la réflexion
(cf. figure 10.6). Dans un premier temps, nous
considérons le cas d'un émetteur et d'un récepteur qui ne sont pas
en ligne de vue.
Figure 10.6:
Effet de multitrajet par diffraction et réflexion.
|
|
L'émetteur envoie un signal cosinusoïdal
A cos(2 fot)
avec
une amplitude et une fréquence fo
constantes. Le signal reçu
au droit du récepteur X(t)
est composé d'une série d'ondes déphasées
et atténuées
fot)
avec
une amplitude et une fréquence fo
constantes. Le signal reçu
au droit du récepteur X(t)
est composé d'une série d'ondes déphasées
et atténuées
X(t) =  Cicos(2 Cicos(2 fot + fot + 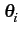 ) ) |
(10.26) |
Cette expression peut s'écrire sous la forme de termes en phase et
en quadrature
| X(t) |
= |
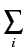 [Aicos(2 [Aicos(2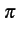 fot) + Bicos(2 fot) + Bicos(2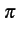 fot + fot + 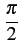 )] )] |
(10.27) |
| |
= |
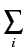 [Aicos(2 [Aicos(2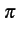 fot) + Bisin(2 fot) + Bisin(2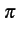 fot)] fot)] |
(10.28) |
| |
= |
XI(t)cos(2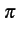 fot) - XQ(t)sin(2 fot) - XQ(t)sin(2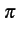 fot) fot) |
(10.29) |
où l'on a défini
XI(t) = 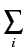 Ai = Ai = 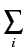 Cicos Cicos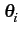 et XQ(t) = et XQ(t) = 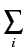 Bi = Bi = 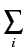 Cisin Cisin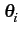 |
(10.30) |
Le canal n'étant pas invariant dans le temps (par exemple en raison
de déplacements), les composantes en phase et en quadrature sont des
fonctions temporelles. D'autre part, X(t)
est la réalisation d'un
processus stochastique qui est la somme de termes indépendants. Dès
lors, en vertu du théorème de la limite centrale, XI(t)
et XQ(t)
représentent des variables aléatoires gaussiennes.
Si l'on veut déterminer l'intensité de champ électrique, il faut analyser
l'évolution de l'amplitude du signal. Cette amplitude est définie
par10.6
R(t) =  , R(t) , R(t)  0 0 |
(10.31) |
quant à la phase, elle vaut
 (t) = tan-1 (t) = tan-1 , ,  (t) (t) 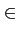 [0, 2 [0, 2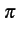 [ [ |
(10.32) |
et donc
X(t) = R(t)cos(2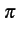 fot + fot +  (t)) (t)) |
(10.33) |
Pour exprimer les densités de probabilité de ces variables aléatoires
à partir de XI(t)
et XQ(t)
, supposons tout d'abord que
les composantes en phase et en quadrature soient des variables gaussiennes
centrées, de même variance
 et non corrélées. Les variables
sont centrées car elles résultent de la somme de variables aléatoires
de type
Cicos
et non corrélées. Les variables
sont centrées car elles résultent de la somme de variables aléatoires
de type
Cicos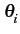 . Or, en supposant que les variables
Ci
et
cos
. Or, en supposant que les variables
Ci
et
cos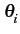 soient indépendantes,
E
soient indépendantes,
E Cicos
Cicos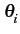
 = E
= E C
C E
E cos
cos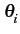
 = 0
si l'on considère un argument uniformément distribué sur l'intervalle
[0, 2
= 0
si l'on considère un argument uniformément distribué sur l'intervalle
[0, 2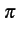 ]
. Physiquement, une moyenne correspond à des contributions
d'amplitude négative, plus précisément à des termes en décalage de
phase de 900
à 2700
.
]
. Physiquement, une moyenne correspond à des contributions
d'amplitude négative, plus précisément à des termes en décalage de
phase de 900
à 2700
.
S'agissant de gaussiennes, la non corrélation entraîne l'indépendance [7, page 162].
La densité de probabilité conjointe est dès lors égale à
Le changement de variables
| xI |
= |
r cos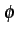 |
(10.35) |
| xQ |
= |
r sin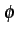 |
(10.36) |
permet de trouver la densité de probabilité conjointe
fR, (r,
(r, )
.
En effet, on sait qu'en toute généralité, un changement de variables
fait intervenir le Jacobien10.7
)
.
En effet, on sait qu'en toute généralité, un changement de variables
fait intervenir le Jacobien10.7
fR, (r, (r,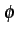 ) = ) = 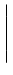 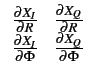  fXI XQ(r cos fXI XQ(r cos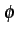 , r sin , r sin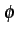 ) ) |
(10.37) |
Dès lors,
fR, (r, (r,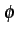 ) ) |
= |
 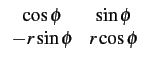  fXI XQ(r cos fXI XQ(r cos , r sin , r sin ) ) |
(10.38) |
| |
= |
 e- e-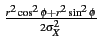 |
(10.39) |
| |
= |
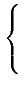 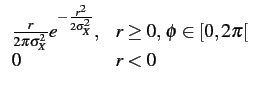 |
(10.40) |
La densité de probabilité marginale des amplitudes s'obtient en intégrant
la densité conjointe sur  . Un calcul simple conduit à
. Un calcul simple conduit à
fR(r) = 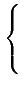 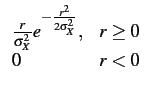 |
(10.41) |
C'est la densité de probabilité de RAYLEIGH.
Elle est illustrée, sous forme normalisée, à la figure 10.7.
Figure 10.7:
Densité de probabilité de RAYLEIGH.
|
|
Les moments de cette loi valent [24]
En particulier,
E r r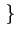 |
= |
 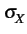 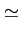 1, 253 x 1, 253 x 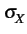 |
(10.43) |
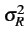 |
= |
 2 - 2 - 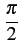  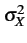 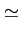 0, 429 x 0, 429 x 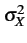 |
(10.44) |
Quant à l'amplitude quadratique moyenne mesurée, elle vaut
Rrms = 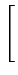  r2 r2 e- e- dr dr![$\displaystyle \left.\vphantom{\int_{0}^{+\infty}r^{2}\frac{r}{2\pi\sigma_{X}^{2}}e^{-\frac{r^{2}}{2\sigma_{X}^{2}}}dr}\right]^{{1/2}}_{}$](img1240.gif) = = 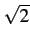 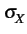 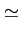 1, 41 x 1, 41 x 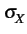 |
(10.45) |
On parle généralement d'évanouissement
lorsque l'amplitude du signal passe en dessous de
Rrms
[21].
Pour obtenir la densité marginale
f (
( )
, on intègre sur
r
de 0
à +
)
, on intègre sur
r
de 0
à + 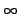 :
:
ce qui signifie que  est une variable aléatoire uniforme et
indépendante de R
, d'où
est une variable aléatoire uniforme et
indépendante de R
, d'où
fR, (r, (r,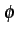 ) = fR(r)f ) = fR(r)f ( (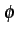 ) ) |
(10.47) |
La figure 10.8 montre l'histogramme de
niveaux de puissance relevés expérimentalement en l'absence d'un trajet
direct. Une approximation de la loi de RAYLEIGH est superposée
à cet histogramme.
Figure 10.8:
Histogramme de niveaux de puissance relevés expérimentalement (d'après
LAPIERRE [20]).
|
|
En présence d'un trajet direct, le signal reçu contient le signal
transmis en ligne droite, en plus du bruit et des copies décalées
et atténuées du signal utile
Z(t) = A cos(2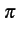 fot + fot + 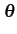 ) + X(t) ) + X(t) |
(10.48) |
Ce cas est évidemment plus favorable que le cas précédent puisque
le récepteur reçoit également le signal en ligne de vue. L'étude menée
ci-après vise à mesurer l'importance de l'ajout du signal direct.
Il ne faudrait pas pour autant en déduire des règles de dimensionnement
car on doit tenir compte des conditions les plus défavorables pour
l'établissement du bilan de puissance, c'est-à-dire en l'absence d'un
trajet direct.
Pour un signal Z(t)
à bande étroite, il est possible de recourir
à la décomposition de RICE
Z(t) = ZI(t)cos(2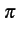 fot) - ZQ(t)sin(2 fot) - ZQ(t)sin(2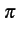 fot) fot) |
(10.49) |
où
| ZI(t) |
= |
A cos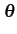 + XI(t) + XI(t) |
(10.50) |
| ZQ(t) |
= |
A sin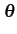 + XQ(t) + XQ(t) |
(10.51) |
En faisant apparaître l'amplitude et la phase,
Z(t) = R(t)cos(2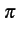 fot + fot +  (t)) (t)) |
(10.52) |
où
R(t) =  , R(t) , R(t)  0 0 |
(10.53) |
et
 (t) = tan-1 (t) = tan-1 , ,  (t) (t) 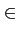 [0, 2 [0, 2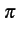 [ [ |
(10.54) |
Dès lors,
| ZI(t) |
= |
R(t)cos (t) (t) |
(10.55) |
| ZQ(t) |
= |
R(t)sin (t) (t) |
(10.56) |
Pour une valeur donnée de 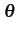 , les variables aléatoires gaussiennes
XI(t)
et XQ(t)
étant indépendantes, elles conservent ce
caractère. Il en résulte que
, les variables aléatoires gaussiennes
XI(t)
et XQ(t)
étant indépendantes, elles conservent ce
caractère. Il en résulte que
| ZI(t) |
= |
N(A cos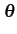 , ,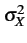 ) ) |
(10.57) |
| ZQ(t) |
= |
N(A sin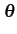 , ,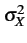 ) ) |
(10.58) |
La probabilité conjointe, conditionnellement à 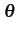 , est donc
, est donc
fZI ZQ(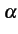 , ,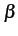 | |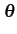 = =  ) = ) =  e- e-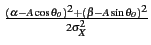 |
(10.59) |
Le même changement de variable fournit le même Jacobien, d'où
fR, (r, (r, | | ) ) |
= |
 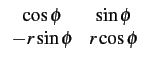  fZI ZQ(r cos fZI ZQ(r cos , r sin , r sin | | ) ) |
(10.60) |
| |
= |
 e- e-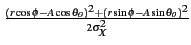 |
(10.61) |
| |
= |
 e- e-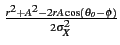 |
(10.62) |
L'intégration sur la phase donne
fR(r| ) ) |
= |
 fR, fR, (r, (r,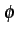 | | )d )d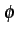 |
(10.63) |
| |
= |
 e- e-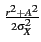  e e d d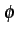 |
(10.64) |
| |
= |
 e- e-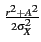 2 2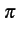 I0 I0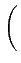 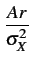  |
(10.65) |
où I0(x)
est la fonction de BESSEL modifiée d'ordre 0
telle que
La fonction I0(x)
est représentée à la figure 10.9.
Figure 10.9:
Fonction de BESSEL modifiée de première espèce d'ordre 0.
|
|
Remarquons que cette densité de probabilité est indépendante de la
phase initiale
 . On peut donc supprimer la condition
en
. On peut donc supprimer la condition
en
 pour aboutir à
pour aboutir à
fR(r) =  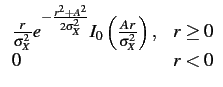 |
(10.68) |
Il s'agit de la densité de probabilité de RICE;
elle est illustrée (sous forme normalisée) à la figure 10.10.
Lorsque A = 0
, il s'agit de la loi de RAYLEIGH.
Figure 10.10:
Densité de probabilité de RICE (pour différentes valeurs de
a =  ).
).
|
|
Notes
- ...
par10.6
- Les résultats suivants résultent de la décomposition en composantes
de RICE et de la représentation par un passe-bas équivalent
d'un signal passe-bande.
- ... Jacobien10.7
- Voir par exemple PAPOULIS [24, page 143] pour
une démonstration.
Marc Van Droogenbroeck. Tous droits réservés.
2007-10-27

![]() fot)
fot)
![]() Cicos(2
Cicos(2![]() fot +
fot + ![]() )
)![]() [Aicos(2
[Aicos(2![]() fot) + Bicos(2
fot) + Bicos(2![]() fot +
fot + ![]() )]
)]![]() [Aicos(2
[Aicos(2![]() fot) + Bisin(2
fot) + Bisin(2![]() fot)]
fot)]![]() fot) - XQ(t)sin(2
fot) - XQ(t)sin(2![]() fot)
fot)![]() Ai =
Ai = ![]() Cicos
Cicos![]() et XQ(t) =
et XQ(t) = ![]() Bi =
Bi = ![]() Cisin
Cisin![]()
 , R(t)
, R(t) ![]() 0
0![]() (t) = tan-1
(t) = tan-1 ,
, ![]() (t)
(t) ![]() [0, 2
[0, 2![]() [
[![]() fot +
fot + ![]() (t))
(t))![]()
![]()
![]()
![]() Cicos
Cicos![]()
![]() = E
= E![]() C
C![]() E
E![]() cos
cos![]()
![]() = 0
= 0
![]() ]
]
![]() ,
,![]() ) =
) =  e-
e-![]()
![]()
![]()
![]() (r,
(r,![]() )
)
![]() (r,
(r,![]() ) =
) = ![]()
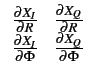
![]() fXI XQ(r cos
fXI XQ(r cos![]() , r sin
, r sin![]() )
)![]() (r,
(r,![]() )
)![]()
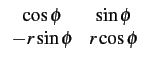
![]() fXI XQ(r cos
fXI XQ(r cos![]() , r sin
, r sin![]() )
) e-
e-![]()
![]()
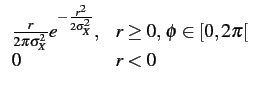
![]()
![]()
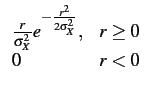
![]() r
r![]() =
= ![]()

![]() r
r![]()
![]()
![]()
![]() 1, 253 x
1, 253 x ![]()
![]()
![]() 2 -
2 - ![]()
![]()
![]()
![]() 0, 429 x
0, 429 x ![]()
![]()
![]() r2
r2 e-
e-![]() dr
dr![]() =
= ![]()
![]()
![]() 1, 41 x
1, 41 x ![]()
![]() (
(![]() )
)
![]()
![]() (
(![]() ) =
) = ![]() ,
, ![]()
![]() [0, 2
[0, 2![]() [
[![]()
![]() (r,
(r,![]() ) = fR(r)f
) = fR(r)f![]() (
(![]() )
)![]() fot +
fot + ![]() ) + X(t)
) + X(t)![]() fot) - ZQ(t)sin(2
fot) - ZQ(t)sin(2![]() fot)
fot)![]() + XI(t)
+ XI(t)![]() + XQ(t)
+ XQ(t)![]() fot +
fot + ![]() (t))
(t)) , R(t)
, R(t) ![]() 0
0![]() (t) = tan-1
(t) = tan-1 ,
, ![]() (t)
(t) ![]() [0, 2
[0, 2![]() [
[![]() (t)
(t)![]() (t)
(t)![]()
![]() ,
,![]() )
)![]() ,
,![]() )
)![]()
![]() ,
,![]() |
|![]() =
= ![]() ) =
) =  e-
e-![]()
![]() (r,
(r,![]() |
|![]() )
)![]()
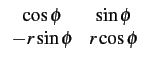
![]() fZI ZQ(r cos
fZI ZQ(r cos![]() , r sin
, r sin![]() |
|![]() )
) e-
e-![]()
 e-
e-![]()
![]() )
)![]() fR,
fR,![]() (r,
(r,![]() |
|![]() )d
)d![]()
 e-
e-![]()
![]() e
e![]() d
d![]()
 e-
e-![]() 2
2![]() I0
I0![]()
![]()
![]()
![]()

![]()
![]()

![]()
![]()
![]()