.
Figure 10.11:
Effet DOPPLER.
|
|
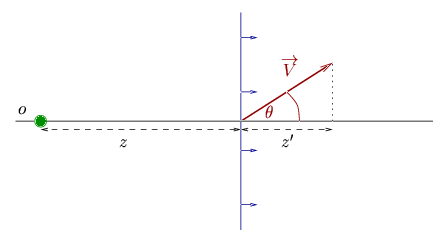
Considérons que l'onde reçue par le mobile est une onde plane et que
le mobile se déplace dans une direction orientée d'un angle 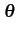 .
Le déplacement du mobile par rapport au front d'onde créée une distorsion
de la fréquence apparente qui porte le nom d'effet DOPPLER.
La distorsion est proportionnelle au déplacement dans l'axe perpendiculaire
au front d'onde.
.
Le déplacement du mobile par rapport au front d'onde créée une distorsion
de la fréquence apparente qui porte le nom d'effet DOPPLER.
La distorsion est proportionnelle au déplacement dans l'axe perpendiculaire
au front d'onde.
Prenons le cas d'une source qui émet un champ électrique sinusoïdal
de fréquence fc
. En l'absence de mouvement, le champ reçu au
droit du mobile vaut, suivant la théorie des ondes [25],
E(t) = E0ej(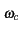 t- t-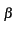 z) z) |
(10.69) |
avec
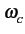 = 2
= 2 fc
et le nombre d'onde
fc
et le nombre d'onde
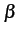 =
= 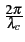 .
Si le mobile est animé d'un mouvement à vitesse
.
Si le mobile est animé d'un mouvement à vitesse
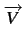 dans
la direction
dans
la direction 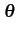 . Le champ reçu devient
. Le champ reçu devient
| E(t) |
= |
E0ej(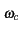 t- t-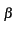 z- z-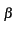 z') z') |
(10.70) |
| |
= |
E0ej(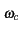 t- t-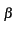 z- z-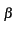 Vt cos Vt cos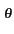 ) ) |
(10.71) |
| |
= |
E0ej2 (fc- (fc-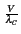 cos cos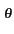 )t-j )t-j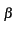 z z |
(10.72) |
Le déplacement du mobile entraîne donc une distorsion de fréquence
d'amplitude
appelée fréquence DOPPLER. Comme V
et 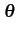 fluctuent
au cours du temps, on assiste à une distorsion de fréquence variable
-et donc de phase- pour l'analyse de laquelle il faudra également
recourir à des outils statistiques. La modification de la fréquence
porteuse dans une place de fréquences porte le nom d'étalement DOPPLER.
La figure 10.12 montre les spectres à l'émission
et à la réception résultant de l'effet DOPPLER.
fluctuent
au cours du temps, on assiste à une distorsion de fréquence variable
-et donc de phase- pour l'analyse de laquelle il faudra également
recourir à des outils statistiques. La modification de la fréquence
porteuse dans une place de fréquences porte le nom d'étalement DOPPLER.
La figure 10.12 montre les spectres à l'émission
et à la réception résultant de l'effet DOPPLER.
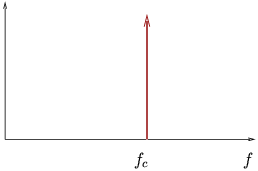
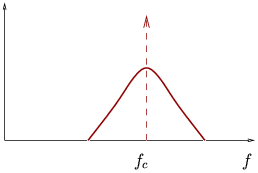
Figure 10.12:
Étalement DOPPLER.
| Spectre à l'émission |
Spectre à la réception |
|
|
|
Exemple. Prenons le cas d'un mobile GSM (
900 [MHz]
)
se déplaçant à 120km/h
. La fréquence DOPPLER maximale intervient
lorsque le mobile se déplace dans l'axe de propagation de l'onde,
c'est-à-dire pour
cos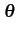 = 1
. Dans ce cas,
fD = fm = V
= 1
. Dans ce cas,
fD = fm = V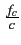 =
= 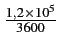 x
x 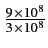 = 100 [Hz]
.
La fréquence instantanée est donc comprise dans un intervalle de largeur
200 [Hz]
.
= 100 [Hz]
.
La fréquence instantanée est donc comprise dans un intervalle de largeur
200 [Hz]
.
L'allure de l'étalement DOPPLER a un impact significatif sur
les statistiques d'évanouissement. Pour en déterminer l'expression,
nous partons d'une hypothèse quant à la distribution des angles d'arrivée
dans le plan horizontal des trajets multiples. Le modèle le plus simple
consiste à considérer une variable aléatoire d'angle d'arrivée 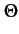 dont la densité de probabilité
f
dont la densité de probabilité
f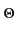 (
(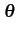 )
est uniformément
distribuée sur l'intervalle
[0, 2
)
est uniformément
distribuée sur l'intervalle
[0, 2 ]
.
]
.
La puissance moyenne récoltée dans un secteur angulaire d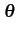 pour une antenne de gain G(
pour une antenne de gain G(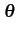 )
vaut
)
vaut
En associant un secteur angulaire à une contribution spécifique de
l'étalement DOPPLER, la puissance correspondante en termes
de fréquence vaut
PR(f )= 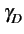 (f ) df (f ) df |
(10.75) |
On remarquera aisément que deux secteurs angulaires d'orientation
opposée contribuent à une même fréquence. Dès lors,
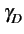 (f ) df = G( (f ) df = G(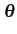 ) f ) f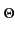 ( (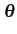 ) d ) d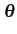 + G(- + G(- 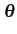 ) f ) f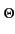 (- (- 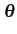 ) d ) d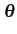 |
(10.76) |
Ce qui mène à
Par la relation 10.73,
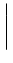 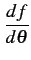 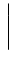 |
= |
fm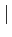 -sin -sin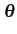 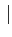 |
(10.78) |
| |
= |
fm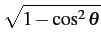 |
(10.79) |
| |
= |
fm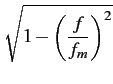 |
(10.80) |
Finalement, en prenant une antenne de gain symétrique, le spectre
vaut
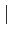 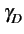 (f ) (f )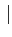 = = 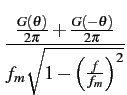 = = 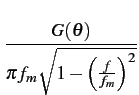 pour pour 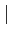 f f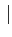 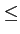 fm fm |
(10.81) |
et 0
pour
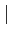 f
f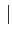 > fm
. Cette forme de spectre porte le nom
de spectre DOPPLER
classique; elle est illustrée à la figure 10.13.
> fm
. Cette forme de spectre porte le nom
de spectre DOPPLER
classique; elle est illustrée à la figure 10.13.
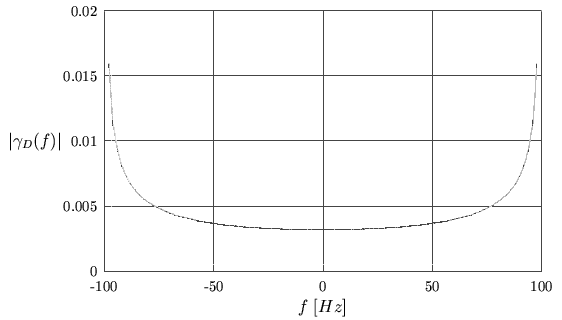
Figure:
Spectre DOPPLER classique (
fc = 900 [MHz]
,
V = 100 [km/h]
et G = 1
).
|
|
Bien que leur obtention soit mathématiquement complexe, il existe
des expressions des densités spectrales de la phase du signal, de
la fréquence instantanée, de l'enveloppe et d'autres quantités encore.
En particulier, l'analyse de l'enveloppe montre que sa fonction d'autocorrélation
se resserre lorsque la vitesse augmente, ce qui signifie que les enveloppes
prises à deux temps voisins sont moins corrélées et donc que l'évanouissement
marque des sauts plus brusques [1].
Marc Van Droogenbroeck. Tous droits réservés.
2007-10-27
![]()
![]() t-
t-![]() z)
z)![]() = 2
= 2![]() fc
fc
![]() =
= ![]()
![]()
![]()
![]() t-
t-![]() z-
z-![]() z')
z')![]() t-
t-![]() z-
z-![]() Vt cos
Vt cos![]() )
)![]() (fc-
(fc-![]() cos
cos![]() )t-j
)t-j![]() z
z![]()
![]() = 1
= 1
![]() =
= 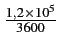 x
x ![]() = 100 [Hz]
= 100 [Hz]
![]()
![]() (
(![]() )
)
![]() ]
]
![]()
![]() )
)
![]() ) = G(
) = G(![]() ) f
) f![]() (
(![]() ) d
) d![]()
![]() (f ) df
(f ) df![]() (f ) df = G(
(f ) df = G(![]() ) f
) f![]() (
(![]() ) d
) d![]() + G(-
+ G(- ![]() ) f
) f![]() (-
(- ![]() ) d
) d![]()
![]()
![]() (f )
(f )![]() =
= 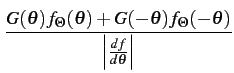
![]()
![]()
![]()
![]() -sin
-sin![]()
![]()
![]()
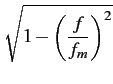
![]()
![]() (f )
(f )![]() =
= 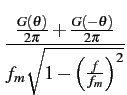 =
= 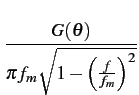 pour
pour ![]() f
f![]()
![]() fm
fm![]() f
f![]() > fm
> fm