Soit une série de N
échantillons
{x[0], x[1], ..., x[N - 1]}
obtenus par échantillonnage d'un processus stochastique. Nous supposons
que cette séquence est stationnaire et ergodique. Il faut estimer
déterminer certains paramètres relatifs à cette séquence telle que
la moyenne 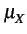 , la covariance CXX(k)
ou
la densité spectrale de puissance
, la covariance CXX(k)
ou
la densité spectrale de puissance
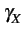 (F)
. Ces paramètres,
moyennes d'ensemble, sont des paramètres déterministes. Si l'on disposait
d'un réalisation s'étendant sur tout l'axe temporel, il serait aisé
de les calculer en vertu de l'hypothèse d'ergodisme. En pratique,
la durée d'observation est finie; on dispose par exemple de
{x[0], x[1], ..., x[N - 1]}
.
C'est la durée d'observation qui pose problème, l'absence d'ergodisme
ne garantit plus l'égalité entre la moyenne ensembliste et la moyenne
temporelle.
(F)
. Ces paramètres,
moyennes d'ensemble, sont des paramètres déterministes. Si l'on disposait
d'un réalisation s'étendant sur tout l'axe temporel, il serait aisé
de les calculer en vertu de l'hypothèse d'ergodisme. En pratique,
la durée d'observation est finie; on dispose par exemple de
{x[0], x[1], ..., x[N - 1]}
.
C'est la durée d'observation qui pose problème, l'absence d'ergodisme
ne garantit plus l'égalité entre la moyenne ensembliste et la moyenne
temporelle.
Sous-sections
Marc Van Droogenbroeck. Tous droits réservés.
2007-10-27
![]()
![]() (F)
(F)