Table des matières of 1.3.3 Estimateur à maximum de vraisemblance

1.3.3.1 Intervalles de confiance

1.3.3 Estimateur à maximum de vraisemblance

Une classe importante d'estimateurs est celle des estimateurs de vraisemblance maximale. Précisons d'emblée que cette technique ne s'applique que pour estimer des paramètres d'une densité de probabilité de forme analytique connue, mais dépendant de ces paramètres. Elle est sans intérêt si cette forme analytique n'est pas connue.

Soient {X[0], X[1], ..., X[N - 1]} les variables aléatoires dont on pourra faire une observation. La densité de probabilité jointe de ces variables peut dépendre de p paramètres { $\alpha_{{1}}^{}$ , $\alpha_{{2}}^{}$ , ..., $\alpha_{{p}}^{}$ }

f (X[0], X[1], ..., X[N - 1]; $\displaystyle \alpha_{{1}}^{}$ , $\displaystyle \alpha_{{2}}^{}$ , ..., $\displaystyle \alpha_{{p}}^{}$ )

(1.46)

Elle est appelée fonction de vraisemblance de ces paramètres lorsqu'on y insère les valeurs observées {x[0], x[1], ..., x[N - 1]} .

L'estimateur à maximum de vraisemblance des paramètres { $\alpha_{{1}}^{}$ , $\alpha_{{2}}^{}$ , ..., $\alpha_{{p}}^{}$ } consiste à calculer les valeurs { $\widehat{{\alpha}}_{{1}}^{}$ , $\widehat{{\alpha}}_{{2}}^{}$ , ..., $\widehat{{\alpha}}_{{p}}^{}$ } qui maximisent la fonction de vraisemblance. On obtient donc les estimations en cherchant la solution du système de p équations à p inconnues

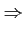$\displaystyle \widehat{{\alpha}}_{{i}}^{}$ = $\displaystyle \alpha_{{i}}^{}$ $\displaystyle \Rightarrow$ $\displaystyle {\frac{{\partial f}}{{\partial\alpha_{i}}}}$ = 0 pour i = 1, 2, p

(1.47)

sous réserve de dérivabilité et d'unicité du maximum.

1.3.3.1 Intervalles de confiance

Cette notion est liée à la technique de l'estimation à maximum de vraisemblance. Cette technique conduit à une formule analytique bien déterminée, du type

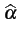$\displaystyle \widehat{{\alpha}}$ = S(x[0], x[1], ..., x[N - 1])

(1.48)

Supposons un instant que la densité de probabilité de la variable aléatoire $\widehat{{\alpha}}$ soit connue. Alors, étant donné un nombre $\epsilon$ ( 0 < $\epsilon$ < 1 ), il est possible de calculer le plus petit intervalle [ $\alpha_{{1}}^{}$ , $\alpha_{{2}}^{}$ ] tel que

p( $\displaystyle \alpha_{{1}}^{}$ < $\displaystyle \widehat{{\alpha}}$ - $\displaystyle \alpha$ < $\displaystyle \alpha_{{2}}^{}$ ) = 1 - $\displaystyle \epsilon$

(1.49)

que l'on peut encore écrire

p( $\displaystyle \widehat{{\alpha}}$ - $\displaystyle \alpha_{{2}}^{}$ < $\displaystyle \alpha$ < $\displaystyle \widehat{{\alpha}}$ - $\displaystyle \alpha_{{1}}^{}$ ) = 1 - $\displaystyle \epsilon$

(1.50)

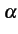Bien que ce soit $\widehat{{\alpha}}$ qui est la variable aléatoire et que $\alpha$ soit une variable certaine, mais inconnue, on a tendance à interpréter cette relation comme la probabilité que 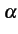$\alpha$ appartienne à l'intervalle [ $\widehat{{\alpha}}$ - $\alpha_{{2}}^{}$ , $\widehat{{\alpha}}$ - $\alpha_{{1}}^{}$ ] .

Après observation, on aura obtenu une certaine valeur (réalisation) $\widehat{{\alpha}}_{{0}}^{}$ de $\widehat{{\alpha}}$ . Le plus petit intervalle [ $\widehat{{\alpha}}_{{0}}^{}$ - $\alpha_{{2}}^{}$ , $\widehat{{\alpha}}_{{0}}^{}$ - $\alpha_{{1}}^{}$ ] tel que

p( $\displaystyle \widehat{{\alpha}}_{{0}}^{}$ - $\displaystyle \alpha_{{2}}^{}$ < $\displaystyle \alpha$ < $\displaystyle \widehat{{\alpha}}_{{0}}^{}$ - $\displaystyle \alpha_{{1}}^{}$ ) = 1 - $\displaystyle \epsilon$

(1.51)

ce qui revient à

$\displaystyle \int_{{\widehat{\alpha}_{0}-\alpha_{2}}}^{{\widehat{\alpha}_{0}-\alpha_{1}}}$ F( $\displaystyle \widehat{{\alpha}}$ )d $\displaystyle \widehat{{\alpha}}$ = 1 - $\displaystyle \epsilon$

(1.52)

est appelé intervalle de confiance. Cet intervalle est interprété comme celui dans lequel on risque de trouver la valeur vraie $\widehat{{\alpha}}$ avec une probabilité 1 - $\epsilon$ ; cependant, une telle interprétation n'étant pas correcte, on utilise le vocable confiance pour la quantité 1 - $\epsilon$ . On parle ainsi d'intervalle de confiance à 90% ou à 99% .