. La moyenne arithmétique
des échantillons
semble être un estimateur raisonnable.
En prenant l'espérance mathématique des deux membres de cette équation,
on a
et l'on voit que cet estimateur est non biaisé.
Essayons à présent d'en déterminer la variance. Soustrayant membre
à membre les deux équations précédentes, il vient
et ensuite
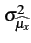 |
= |
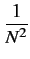 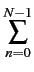 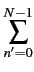 E E![$\displaystyle \left\{\vphantom{ (x[n]-\mu_{x})(x[n']-\mu_{x})}\right.$](img165.gif) (x[n] - (x[n] -  )(x[n'] - )(x[n'] -  ) )![$\displaystyle \left.\vphantom{ (x[n]-\mu_{x})(x[n']-\mu_{x})}\right\}$](img166.gif) |
(1.56) |
| |
= |
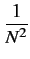 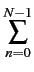 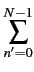 Cxx[n - n'] Cxx[n - n'] |
(1.57) |
| |
= |
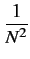 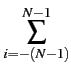 (N - (N - 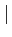 i i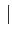 )Cxx[i] )Cxx[i] |
(1.58) |
Cette dernière expression s'obtient en observant que, dans la double
somme 1.57, la différence n - n'
prend N
fois la valeur 0
, N - 1
fois les valeurs 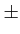 1
, etc.
1
, etc.
Cette expression met en évidence un problème courant dans le domaine
de l'estimation. Alors qu'on tente ici d'estimer un moment du premier
ordre, il faudrait connaître les moments du deuxième ordre pour déterminer
la précision de l'estimateur: plus généralement, la précision de l'estimateur
des moments d'un ordre déterminé dépend des moments d'un ordre supérieur.
Ceux-ci sont logiquement inconnus, et il faudra les estimer eux-mêmes
pour avoir une idée de la précision de l'estimateur.
Revenons au cas présent. La double somme 1.57
comprend N2
termes et, d'une manière générale, il se pourrait
que la variance de l'estimateur ne décroisse pas lorsque la durée
N
de l'enregistrement augmente. Cependant, si la fonction de covariance
Cxx[i]
décroît avec i
et, plus précisément, si
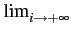 Cxx[i] = 0
, la simple somme
apparaissant dans l'équation 1.58 croît proportionnellement
à N
lorsque
N
Cxx[i] = 0
, la simple somme
apparaissant dans l'équation 1.58 croît proportionnellement
à N
lorsque
N 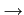 +
+ 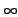 . Dans ce cas, la variance de
l'estimateur de
. Dans ce cas, la variance de
l'estimateur de
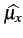 décroît comme
décroît comme
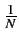 et l'estimateur est consistant. Ainsi, si l'on savait que x[n]
est un bruit blanc d'intensité
et l'estimateur est consistant. Ainsi, si l'on savait que x[n]
est un bruit blanc d'intensité
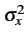 , on aurait
, on aurait
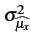 =
= 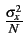 .
.
On pourrait croire, à tort, que la moyenne arithmétique est le seul
estimateur de la moyenne. En fait, dans les cas où l'on ne dispose
que d'un faible nombre d'échantillons, il est intéressant de recourir
à la médiane. Si pour certaines distributions aléatoires,
par exemple la gaussienne, médiane et moyenne sont confondues, il
n'empêche qu'en pratique la médiane est parfois préférée à la moyenne
arithmétique.
Marc Van Droogenbroeck. Tous droits réservés.
2007-10-27
![]()
![]() =
= ![]()
![]() x[n]
x[n]![]()
![]()
![]()
![]() =
= ![]()
![]()
![]() - E
- E![]()
![]()
![]() =
= ![]()
![]() (x[n] -
(x[n] - ![]() )
)![]() 1
1
![]() Cxx[i] = 0
Cxx[i] = 0
![]() +
+ ![]()
![]()
![]()
![]()
![]() =
= ![]()