Par calcul, on montre aisément que
qui n'est rien d'autre que la transformée de FOURIER au carré
de l'enregistrement, prolongé par des zéros.
Cet estimateur est appelé périodigramme.
Il est malheureusement biaisé et
E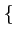 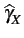 (F) (F)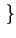 = = 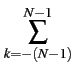 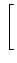 1 - 1 - 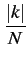 ![$\displaystyle \left.\vphantom{1-\frac{\left\vert k\right\vert}{N}}\right]$](img202.gif) 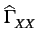 [k]e-2 [k]e-2 jFk jFk |
(1.74) |
Le périodigramme est un estimateur asymptotiquement sans biais de
la densité spectrale de puissance: pour une durée d'observation N
suffisamment grande,
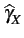 (F)
fluctue autour de
la vraie valeur de
(F)
fluctue autour de
la vraie valeur de
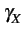 (F)
. Par contre, l'amplitude des fluctuations,
qui est donné par la variance de
(F)
. Par contre, l'amplitude des fluctuations,
qui est donné par la variance de
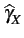 (F)
, ne tend
pas vers 0
lorsque N
tend vers l'infini. Plus précisément, on
montre que cette variance est de l'ordre de grandeur de la valeur
à estimer. La figure 1.9 montre quatre
périodigrammes et une certaine densité spectrale théorique. On observe
que, malgré l'allongement de la durée d'observation, l'amplitude des
fluctuations ne diminue pas.
(F)
, ne tend
pas vers 0
lorsque N
tend vers l'infini. Plus précisément, on
montre que cette variance est de l'ordre de grandeur de la valeur
à estimer. La figure 1.9 montre quatre
périodigrammes et une certaine densité spectrale théorique. On observe
que, malgré l'allongement de la durée d'observation, l'amplitude des
fluctuations ne diminue pas.
Figure 1.9:
Fluctuations du périodigramme en fonction de la période totale d'observation
N
.
|
|
En pratique, on applique la transformée discrète. Dès lors,
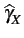 (Fk) = (Fk) = 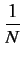 ![$\displaystyle \left\Vert\vphantom{ \sum_{n=0}^{N-1}x[n]e^{-2\pi jkn/N}}\right.$](img205.gif) 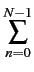 x[n]e-2 x[n]e-2 jkn/N jkn/N![$\displaystyle \left.\vphantom{ \sum_{n=0}^{N-1}x[n]e^{-2\pi jkn/N}}\right\Vert^{{2}}_{}$](img206.gif) |
(1.75) |
Marc Van Droogenbroeck. Tous droits réservés.
2007-10-27
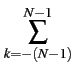
![]() (F)
(F)
![]() (F)
(F)
![]() (F)
(F)
![]() (Fk) =
(Fk) = ![]()
![]()
![]() x[n]e-2
x[n]e-2![]() jkn/N
jkn/N![]()