Prenons un signal passe-bande g(t)
. On montre le théorème d'échantillonnage
uniforme suivant pour les signaux passe-bande.
Théorème 10
Une fonction g(t)
à énergie finie et à spectre limité, c'est-à-dire
dont la transformée de FOURIER
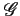 (f )
est de largeur
W
, et qui admet une borne supérieure fu
, est entièrement
déterminée par ses échantillons g[nTs]
,
n
(f )
est de largeur
W
, et qui admet une borne supérieure fu
, est entièrement
déterminée par ses échantillons g[nTs]
,
n  { -
{ -  , +
, + 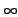 }
si la fréquence d'échantillonnage fs
vaut
}
si la fréquence d'échantillonnage fs
vaut
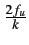 ,
tel que k
est le plus grand entier strictement inférieur à
,
tel que k
est le plus grand entier strictement inférieur à
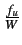 .
.
Il est à noter que toutes les fréquences d'échantillonnage ne conviennent
pas sauf si elles sont strictement supérieures à 2fu
.
Démonstration
On sait que le spectre d'un signal échantillonné gs(t)
est périodique centré sur les multiples ifs
:
Dans notre cas, le signal est de type passe-bande. L'échantillonnage
pourrait amener un chevauchement des copies des spectres si l'on n'y
prend garde. Prenons une fréquence d'échantillonnage fs
définie
par
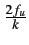 . Pour éviter tout repli de spectre, il faut
impérativement que fs > 2W
. Dès lors, on obtient
. Pour éviter tout repli de spectre, il faut
impérativement que fs > 2W
. Dès lors, on obtient
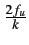 > 2W
,
ce qui implique
k <
> 2W
,
ce qui implique
k < 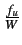 .
.
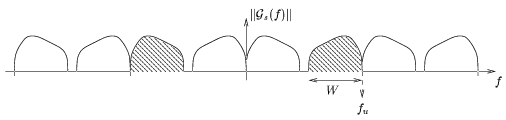
Exemple. Considérons un signal
W = 20 [kHz]
et
fu = 105 [kHz]
. Par application du théorème, k < 5, 25
. Autrement
dit, la fréquence d'échantillonnage
fs = 42 [kHz]
convient. La
figure 2.2 représente le signal échantillonné
dans le domaine spectral. On est évidemment loin de la fréquence de
NYQUIST qui aurait prévalu s'il ne s'agissait d'un signal passe-bande.
Figure 2.2:
Signal passe-bande et signal après échantillonnage.
|
|
Plusieurs remarques s'imposent:
- S'il est vrai que le théorème garantit que soit préservée la bande
de fréquence utile, il ne dit rien quant à la position des copies
du spectre. On sait tout au plus que le spectre doit être symétrique
puisque le signal échantillonné est réel. Il serait pourtant fort
agréable de n'avoir que la partie située à droite ou à gauche de l'origine
et de la centrer sur l'origine. On pourrait alors utiliser cette copie
pour des opérations de type passe-bas, nettement plus faciles à réaliser.
Précisons toutefois que la partie qui aboutirait près de l'origine
n'est pas nécessairement symétrique; le filtrage de la composante
à basse fréquence fournira donc un signal complexe.
- Le théorème ne fait nullement intervenir le concept de fréquence porteuse
même si la majorité des signaux de type passe-bande sont le résultat
d'une phase de modulation.
Marc Van Droogenbroeck. Tous droits réservés.
2007-10-27
![]() fs
fs![]()
![]() (f - ifs)
(f - ifs)![]()
![]() > 2W
> 2W
![]()