Table des matières of 2.3.1 Illustration: démodulation d'un signal FM

2.3.1 Illustration: démodulation d'un signal FM

La méthode de démodulation présentée ici est une illustration de l'utilisation du signal analytique et de l'enveloppe complexe. Elle utilise un circuit électrique appelé discriminateur de fréquences, dont l'amplitude instantanée de la sortie est directement proportionnelle à la fréquence instantanée du signal FM d'entrée. Étant donné que la fréquence instantanée d'un signal FM est donnée par

f_i(t) = f_c + k_fm(t)

(2.64)

m(t)

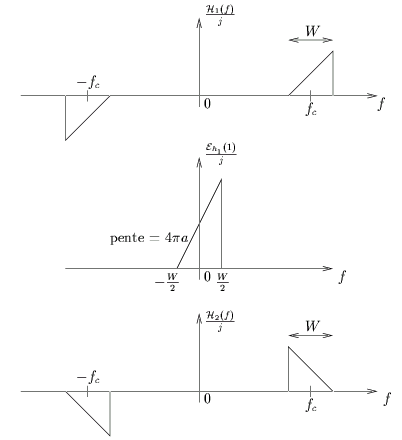
Un discriminateur de fréquence est composé d'un filtre en forme de rampe suivi d'un détecteur d'enveloppe. Un filtre rampe idéal est caractérisé par une transmittance purement imaginaire, variant linéairement avec la fréquence à l'intérieur d'un intervalle de fréquence fixé. Il s'agit ni plus ni moins que de l'expression de la dérivée en termes fréquentiels. Considérons donc le filtre

$\displaystyle \mathcal {H}$ ₁ $\displaystyle \left(\vphantom{f}\right.$ f $\displaystyle \left.\vphantom{f}\right)$ = $\displaystyle \left\{\vphantom{ \begin{array}{ccc} 2\pi ja\left(f-f_{c}+\frac{W... ...W}{2}\leq f\leq-f_{c}+\frac{W}{2} 0 & & \textrm{ailleurs}\end{array}}\right.$ $\displaystyle \begin{array}{ccc} 2\pi ja\left(f-f_{c}+\frac{W}{2}\right) & & f_... ...}-\frac{W}{2}\leq f\leq-f_{c}+\frac{W}{2} 0 & & \textrm{ailleurs}\end{array}$

(2.65)

où a est une constante. La fonction de transfert $\mathcal {H}$ ₁(f ) est représentée à la figure 2.6.a.

**Figure 2.6:** Réponse fréquentielle du filtre rampe idéal.

Nous allons à présent déterminer la réponse de ce filtre, notée s₁(t) , lorsqu'on lui applique en entrée un signal FM de fréquence porteuse f_c et dont le spectre est négligeable en dehors de l'intervalle de fréquence [f_c - W/2, f_c + W/2] . Pour évaluer s₁(t) , il est intéressant d'utiliser la procédure décrite au paragraphe précédent. Nous allons donc remplacer le filtre rampe par un filtre passe-bas équivalent et utiliser la notion d'enveloppe complexe. La transformée de FOURIER de l'enveloppe complexe de la réponse impulsionnelle du filtre est simplement donnée par

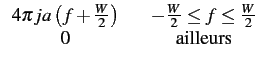$\displaystyle \mathcal {E}$ _h₁ $\displaystyle \left(\vphantom{f}\right.$ f $\displaystyle \left.\vphantom{f}\right)$ = $\displaystyle \left\{\vphantom{ \begin{array}{ccc} 4\pi ja\left(f+\frac{W}{2}\r... ...-\frac{W}{2}\leq f\leq\frac{W}{2} 0 & & \textrm{ailleurs}\end{array}}\right.$ $\displaystyle \begin{array}{ccc} 4\pi ja\left(f+\frac{W}{2}\right) & & -\frac{W}{2}\leq f\leq\frac{W}{2} 0 & & \textrm{ailleurs}\end{array}$

(2.66)

qui est montrée à la figure 2.6.b. Le signal FM d'entrée est défini par

s $\displaystyle \left(\vphantom{t}\right.$ t $\displaystyle \left.\vphantom{t}\right)$ = A_ccos $\displaystyle \left(\vphantom{2\pi f_{c}t+2\pi k_{f}\int_{0}^{t}m\left(t'\right) dt'}\right.$ 2 $\displaystyle \pi$ f_ct + 2 $\displaystyle \pi$ k_f $\displaystyle \int_{{0}}^{{t}}$ m $\displaystyle \left(\vphantom{t'}\right.$ t' $\displaystyle \left.\vphantom{t'}\right)$ dt' $\displaystyle \left.\vphantom{2\pi f_{c}t+2\pi k_{f}\int_{0}^{t}m\left(t'\right) dt'}\right)$

(2.67)

Le signal analytique s_a(t) relatif à s(t) est simplement égal à

s_a(t) = A_ce^{2jf_ct+2jk_fm(t') dt'}

(2.68)

et l'enveloppe complexe du signal FM se réduit à

e_s $\displaystyle \left(\vphantom{t}\right.$ t $\displaystyle \left.\vphantom{t}\right)$	=	s_a(t) e^-2jf_ct	(2.69)
	=	A_ce^{2jk_fm(t') dt'}	(2.70)

Étant donnée la théorie développée au paragraphe précédent, le spectre de l'enveloppe complexe du signal de sortie, noté $\mathcal {E}$ _s₁(f ) , est donné par

$\displaystyle \mathcal {E}$ _s₁ $\displaystyle \left(\vphantom{f}\right.$ f $\displaystyle \left.\vphantom{f}\right)$	=	$\displaystyle {\frac{{1}}{{2}}}$ $\displaystyle \mathcal {E}$ _h₁ $\displaystyle \left(\vphantom{f}\right.$ f $\displaystyle \left.\vphantom{f}\right)$ $\displaystyle \mathcal {E}$ _s $\displaystyle \left(\vphantom{f}\right.$ f $\displaystyle \left.\vphantom{f}\right)$	(2.71)
	=	$\displaystyle \left\{\vphantom{ \begin{array}{ccc} 2\pi ja\left(f+\frac{W}{2}\r... ...t[-\frac{W}{2},\frac{W}{2}\right]\\ 0 & & \textrm{ailleurs}\end{array}}\right.$ $\displaystyle \begin{array}{ccc} 2\pi ja\left(f+\frac{W}{2}\right)\mathcal{E}_{... ...f\in\left[-\frac{W}{2},\frac{W}{2}\right]\\ 0 & & \textrm{ailleurs}\end{array}$	(2.72)

où $\mathcal {E}$ _s(f ) est la transformée de FOURIER de l'enveloppe complexe de s(t) . Comme la multiplication par 2 $\pi$ jf dans le domaine fréquentiel revient à dériver dans le domaine temporel, il est facile de calculer l'enveloppe complexe du signal de sortie s₁(t) par transformée de FOURIER inverse

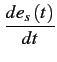e_s₁ $\displaystyle \left(\vphantom{t}\right.$ t $\displaystyle \left.\vphantom{t}\right)$ = a $\displaystyle \left[\vphantom{\frac{de_{s}\left(t\right)}{dt}+\pi jWe_{s}\left(t\right)}\right.$ $\displaystyle {\frac{{de_{s}\left(t\right)}}{{dt}}}$ + $\displaystyle \pi$ jWe_s $\displaystyle \left(\vphantom{t}\right.$ t $\displaystyle \left.\vphantom{t}\right)$ $\displaystyle \left.\vphantom{\frac{de_{s}\left(t\right)}{dt}+\pi jWe_{s}\left(t\right)}\right]$

(2.73)

En introduisant l'expression de e_s(t) dans l'expression précédente, on obtient finalement l'expression temporelle de l'enveloppe complexe du signal de sortie

e_s₁ $\displaystyle \left(\vphantom{t}\right.$ t $\displaystyle \left.\vphantom{t}\right)$ = $\displaystyle \pi$ jWaA_c $\displaystyle \left[\vphantom{1+\frac{2k_{f}}{W}m\left(t\right)}\right.$ 1 + $\displaystyle {\frac{{2k_{f}}}{{W}}}$ m $\displaystyle \left(\vphantom{t}\right.$ t $\displaystyle \left.\vphantom{t}\right)$ $\displaystyle \left.\vphantom{1+\frac{2k_{f}}{W}m\left(t\right)}\right]$ e^{2jk_fm(t') dt'}

(2.74)

La réponse s₁(t) du filtre rampe est alors donnée par

s₁ $\displaystyle \left(\vphantom{t}\right.$ t $\displaystyle \left.\vphantom{t}\right)$	=	Re $\displaystyle \left(\vphantom{e_{s_{1}}\left(t\right)e^{2\pi jf_{c}t}}\right.$ e_s₁ $\displaystyle \left(\vphantom{t}\right.$ t $\displaystyle \left.\vphantom{t}\right)$ e^2jf_ct $\displaystyle \left.\vphantom{e_{s_{1}}\left(t\right)e^{2\pi jf_{c}t}}\right)$	(2.75)
	=	$\displaystyle \pi$ WaA_c $\displaystyle \left[\vphantom{1+\frac{2k_{f}}{W}m\left(t\right)}\right.$ 1 + $\displaystyle {\frac{{2k_{f}}}{{W}}}$ m $\displaystyle \left(\vphantom{t}\right.$ t $\displaystyle \left.\vphantom{t}\right)$ $\displaystyle \left.\vphantom{1+\frac{2k_{f}}{W}m\left(t\right)}\right]$ cos $\displaystyle \left(\vphantom{2\pi f_{c}t+2\pi k_{f}\int_{0}^{t}m\left(t'\right) dt'+\frac{\pi}{2}}\right.$ 2 $\displaystyle \pi$ f_ct + 2 $\displaystyle \pi$ k_f $\displaystyle \int_{{0}}^{{t}}$ m $\displaystyle \left(\vphantom{t'}\right.$ t' $\displaystyle \left.\vphantom{t'}\right)$ dt' + $\displaystyle {\frac{{\pi}}{{2}}}$ $\displaystyle \left.\vphantom{2\pi f_{c}t+2\pi k_{f}\int_{0}^{t}m\left(t'\right) dt'+\frac{\pi}{2}}\right)$	(2.76)

Le signal s₁(t) est un signal modulé hybride dont l'amplitude et la fréquence varient avec le signal modulant m(t) . Cependant, si

$\displaystyle \left\vert\vphantom{\frac{2k_{f}}{W}m\left(t\right)}\right.$ $\displaystyle {\frac{{2k_{f}}}{{W}}}$ m $\displaystyle \left(\vphantom{t}\right.$ t $\displaystyle \left.\vphantom{t}\right)$ $\displaystyle \left.\vphantom{\frac{2k_{f}}{W}m\left(t\right)}\right\vert$ < 1

(2.77)

pour tout t , nous pouvons utiliser un détecteur d'enveloppe pour retrouver les variations d'amplitude de s₁(t) et donc, à un terme constant près, obtenir le signal modulant m(t) . La sortie du détecteur d'enveloppe est alors égale à

$\displaystyle \left\Vert\vphantom{ e_{s_{1}}\left(t\right)}\right.$ e_s₁ $\displaystyle \left(\vphantom{t}\right.$ t $\displaystyle \left.\vphantom{t}\right)$ $\displaystyle \left.\vphantom{ e_{s_{1}}\left(t\right)}\right\Vert$ = $\displaystyle \pi$ WaA_c $\displaystyle \left[\vphantom{1+\frac{2k_{f}}{W}m\left(t\right)}\right.$ 1 + $\displaystyle {\frac{{2k_{f}}}{{W}}}$ m $\displaystyle \left(\vphantom{t}\right.$ t $\displaystyle \left.\vphantom{t}\right)$ $\displaystyle \left.\vphantom{1+\frac{2k_{f}}{W}m\left(t\right)}\right]$

(2.78)

La composante continue $\pi$ WaA_c est proportionnelle à la pente a de la transmittance du filtre rampe. Cela suggère que cette composante continue peut être éliminée en soustrayant à la sortie $\left\Vert\vphantom{ e_{s_{1}}(t)}\right.$ e_s₁(t) $\left.\vphantom{ e_{s_{1}}(t)}\right\Vert$ du détecteur d'enveloppe la sortie d'un second détecteur d'enveloppe précédé par le filtre rampe complémentaire dont la transmittance $\mathcal {H}$ ₂(f ) est représentée à la figure 2.6.c. Ainsi, les enveloppes complexes relatives aux réponses impulsionnelles des deux filtres rampes sont liées par

$\displaystyle \mathcal {E}$ _h₂ $\displaystyle \left(\vphantom{f}\right.$ f $\displaystyle \left.\vphantom{f}\right)$ = $\displaystyle \mathcal {E}$ _h₁ $\displaystyle \left(\vphantom{-f}\right.$ - f $\displaystyle \left.\vphantom{-f}\right)$

(2.79)

Appelons s₂(t) la réponse du filtre rampe complémentaire au signal FM s(t) . Alors, en suivant une procédure similaire à celle qui a été faite pour s₁(t) , nous pouvons déterminer la sortie du second détecteur d'enveloppe

$\displaystyle \left\Vert\vphantom{ e_{s_{2}}\left(t\right)}\right.$ e_s₂ $\displaystyle \left(\vphantom{t}\right.$ t $\displaystyle \left.\vphantom{t}\right)$ $\displaystyle \left.\vphantom{ e_{s_{2}}\left(t\right)}\right\Vert$ = $\displaystyle \pi$ WaA_c $\displaystyle \left[\vphantom{1-\frac{2k_{f}}{W}m\left(t\right)}\right.$ 1 - $\displaystyle {\frac{{2k_{f}}}{{W}}}$ m $\displaystyle \left(\vphantom{t}\right.$ t $\displaystyle \left.\vphantom{t}\right)$ $\displaystyle \left.\vphantom{1-\frac{2k_{f}}{W}m\left(t\right)}\right]$

(2.80)

où e_s₂(t) est l'enveloppe complexe de s₂(t) . La différence entre les sorties des deux détecteurs d'enveloppe est le signal s₀(t) donné par

s₀ $\displaystyle \left(\vphantom{t}\right.$ t $\displaystyle \left.\vphantom{t}\right)$	=	$\displaystyle \left\Vert\vphantom{ e_{s_{1}}\left(t\right)}\right.$ e_s₁ $\displaystyle \left(\vphantom{t}\right.$ t $\displaystyle \left.\vphantom{t}\right)$ $\displaystyle \left.\vphantom{ e_{s_{1}}\left(t\right)}\right\Vert$ - $\displaystyle \left\Vert\vphantom{ e_{s_{2}}\left(t\right)}\right.$ e_s₂ $\displaystyle \left(\vphantom{t}\right.$ t $\displaystyle \left.\vphantom{t}\right)$ $\displaystyle \left.\vphantom{ e_{s_{2}}\left(t\right)}\right\Vert$	(2.81)
	=	4 $\displaystyle \pi$ k_faA_cm $\displaystyle \left(\vphantom{t}\right.$ t $\displaystyle \left.\vphantom{t}\right)$	(2.82)

qui est ainsi débarrassé de toute composante continue.

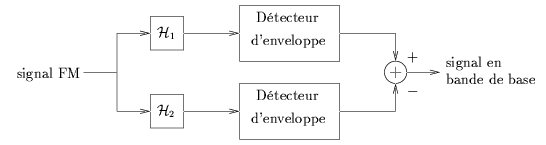
Nous avons ainsi modélisé le discriminateur de fréquence idéal par une paire de filtres rampes, suivis de détecteurs d'enveloppe et d'un sommateur comme le montre la figure 2.7. Ce schéma est appelé discriminateur de fréquence balancé.

**Figure 2.7:** Schéma bloc idéal du discriminateur de fréquence balancé.

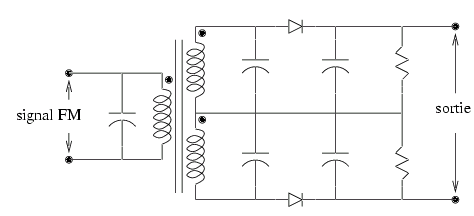
Le schéma idéal de la figure 2.7 peut être approximativement réalisé en utilisant le circuit de la figure 2.8.

**Figure 2.8:** Schéma électrique du discriminateur de fréquence balancé.

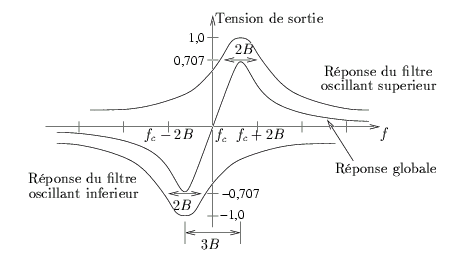
Les circuits résonnant LC supérieur et inférieur sont accordés respectivement sur des fréquences supérieure et inférieure à la fréquence de la porteuse f_c . Les réponses fréquentielles de ces deux circuits résonnants, ainsi que leur réponse combinée, sont représentées à la figure 2.9. La linéarité de la portion utile de la réponse globale, centrée sur f_c , est déterminée par la séparation entre les deux fréquences de résonance. Comme le montre la figure 2.9, une séparation de 3B donne des résultats satisfaisants, où 2B est la bande passante à 3 [dB] de chaque filtre.

**Figure 2.9:** Réponse fréquentielle des deux circuits résonnants [15, page 179].

Cependant, il y aura des distorsions dans le signal de sortie du discriminateur de fréquences, dues au fait que

le spectre du signal FM s(t) n'est pas strictement limité à l'intervalle de fréquence $\left[\vphantom{f_{c}-W/2, f_{c}+W/2}\right.$ f_c - W/2, f_c + W/2 $\left.\vphantom{f_{c}-W/2, f_{c}+W/2}\right]$ ,
les sorties des circuits résonnants ne sont pas strictement à bande limitée et des distorsions peuvent être introduites par les filtres passe-bas RC suivant les diodes dans les détecteurs d'enveloppe,
la réponse fréquentielle des circuits résonnants n'est pas linéaire sur toute la bande de fréquence du signal FM.

Cependant, une conception soignée permet de maintenir les distorsions dans des proportions acceptables.