Sous-sections
Du fait de l'agitation thermique des électrons, une résistance R
portée à une température absolue T
(c'est-à-dire exprimée en degré
KELVIN [K]
) produit à ses bornes une force électromotrice
E(t)
qui est une fonction aléatoire. Cet effet, appelé effet
JOHNSON, fut entre autres étudié par NYQUIST.
L'effort de modélisation consiste à
- décrire le phénomène aléatoire pour une résistance simple,
- analyser l'effet du bruit dans des configurations électriques complexes.
Une résistance R
portée à une température absolue T
[K]
possède
le schéma équivalent de THÉVENIN de la figure 3.1,
comprenant une résistance R
dépourvue de bruit et une force électromotrice
de bruit thermique E(t)
qui est une fonction
aléatoire, stationnaire, centrée, gaussienne et qui est en première
approximation un bruit blanc de densité spectrale de puissance
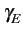 (f )= 2kBTR (f )= 2kBTR |
(3.1) |
où
kB = 1, 38 x 10-23 [J/K]
est la constante
de BOLTZMANN.
Figure 3.1:
Équivalents de THÉVENIN (a) et de NORTON (b) correspondant
au bruit thermique dans une résistance.
|
|
L'équivalent de NORTON fournit quant à lui
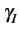 (f )= 2kBTG (f )= 2kBTG |
(3.2) |
L'étude plus détaillée du phénomène de bruit thermique fait apparaître
une dépendance fréquentielle par le biais d'un facteur p(f )
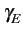 (f )= 2kBTRp(f ) (f )= 2kBTRp(f ) |
(3.3) |
où
p(f )= 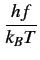 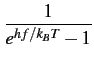 |
(3.4) |
est le facteur de PLANCK [35]. Dans la gamme de
fréquences considérées, il est raisonnable de supposer que la densité
spectrale de puissance est constante.
Considérons à présent le cas d'un dipôle d'impédance interne
complexe Zs
. La densité spectrale de puissance prend
alors la forme
Dès lors, la valeur quadratique moyenne de la force électromotrice
de bruit thermique dans un intervalle
[- f - df, - f]  [f, f + df]
vaut
[f, f + df]
vaut
Marc Van Droogenbroeck. Tous droits réservés.
2007-10-27
![]() (f )= 2kBTR
(f )= 2kBTR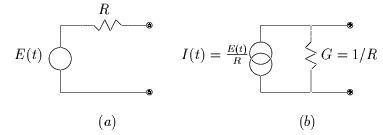
![]() (f )= 2kBTG
(f )= 2kBTG![]() (f )= 2kBTRp(f )
(f )= 2kBTRp(f )![]()
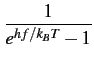
![]() (f )= 2kBTRe
(f )= 2kBTRe![]() Zs(f )
Zs(f )![]()
![]() [f, f + df]
[f, f + df]