Sous-sections
La puissance disponible aux bornes d'un dipôle est un élément essentiel
de conception d'un circuit. En effet, on sait que le transfert maximum
de puissance a lieu à l'adaptation conjuguée de l'impédance de source.
C'est bien évidemment sous ce régime que l'on sera souvent amené à
travailler.
Considérons le cas de signaux sinusoïdaux. La puissance de source
fournie par le dipôle Psf
vaut
Psf = 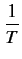 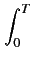 v(t)i(t)dt = v(t)i(t)dt =  Re Re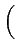 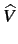 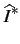 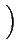 |
(3.8) |
Dans une charge ZL
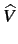 = = 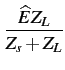 |
(3.9) |
et
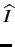 = = 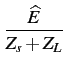 |
(3.10) |
On a donc une puissance
Psf = 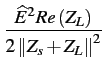 |
(3.11) |
On sait que la puissance fournie par le dipôle est maximale à l'adaptation
conjuguée. Cette puissance, notée Psd
, est appelée puissance
disponible du dipôle; elle vaut
Psd = 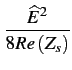 |
(3.12) |
La puissance disponible dépend de la valeur de crête de la force électromotrice
et de la partie réelle du dipôle. C'est donc un invariant pour la
famille des impédances dont la partie résistive est identique.
Dans le cas de processus stochastiques, les relations restent valables
à condition de les formuler entre densités spectrales de puissance.
Examinons la question pour un bruit aléatoire quelconque
et, après application du théorème de WIENER-KINTCHINE,
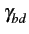 (f )= (f )= 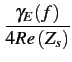 |
(3.14) |
Remarquons que cette formulation est aussi bien valable pour les signaux
utiles délivrés par la source que pour le bruit parasite introduit
par cette même source. Au dénominateur, on retrouve un facteur 4
et non 8
comme dans l'expression 3.12. Cela s'explique
simplement par le fait que la définition de la puissance disponible
Psd
s'appuie sur l'expression de la puissance fournie Psf
,
qui elle fait intervenir les valeurs de crête et donc un facteur
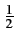 supplémentaire.
supplémentaire.
Exemple. Dans le cas particulier du bruit thermique
La densité spectrale de bruit disponible dépend donc de la température
mais pas de la fréquence; c'est donc un bruit blanc de densité spectrale
uniforme
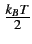 .
.
Le tableau 3.1 reprend les principaux résultats
énoncés dans cette section.
Marc Van Droogenbroeck. Tous droits réservés.
2007-10-27
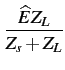
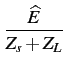
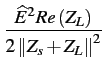
![]()
![]()
![]() V(t)I(t)dt
V(t)I(t)dt![]() (f )=
(f )= 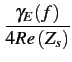
![]()
![]()
![]() Re
Re![]()
![]()
![]()
![]() =
= 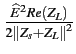
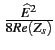
![]()
![]()
![]() V(t)I(t)dt
V(t)I(t)dt
![]() (f )=
(f )= ![]()
![]() (f )=
(f )= ![]()
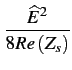
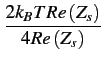 =
=