Sous-sections
Pour décrire convenablement un quadripôle en sortie, il faut impérativement
tenir compte de l'entrée. Ainsi, si l'entrée est un circuit ouvert
ou si elle est court-circuitée, la sortie ne sera généralement pas
la même.
Lors de la caractérisation du bruit du quadripôle, c'est le bruit
interne, produit par le quadripôle, qui nous intéresse. Cette caractérisation
nécessite néanmoins que l'on précise le type de circuit placé à l'entrée.
Alors, plutôt que de considérer un circuit ouvert ou un court-circuit,
on préfère prendre une source de référence proche de la réalité, à
savoir une source de bruit thermique de température ambiante de référence.
Ce choix conduit à la définition du facteur de bruit. Nous
verrons ensuite comment traiter une source différente de la source
de référence.
Définition 20
[Facteur de bruit] L'impédance interne du quadripôle
générateur étant donnée, le facteur de bruit
du quadripôle à la fréquence d'entrée f
, noté F0(f )
, est
le rapport de (1) la densité spectrale de bruit disponible à la sortie
du quadripôle, à la fréquence correspondante, lorsque la température
de bruit du dipôle générateur est
T0 = 290 [K]
à (2) la partie
de cette densité spectrale due au bruit du dipôle générateur à la
fréquence f
.
Dans cette définition, on peut remplacer le terme ``disponible''
par ``fournie par''.
En raison de l'indépendance statistique des bruits, la densité spectrale
de bruit disponible, à une certaine fréquence, à la sortie du quadripôle
est la somme de la densité spectrale de bruit disponible du générateur
multipliée par le gain, à cette même fréquence, et des densités spectrales
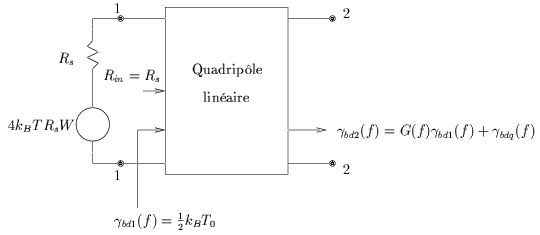
de bruit propres au quadripôle. Considérons pour l'étude analytique
le dessin de la figure 3.4.
Figure 3.4:
Schéma d'un quadripôle bruité.
|
|
Si l'on considère un dipôle générateur porté à la température T0
en entrée, on peut écrire la densité spectrale disponible à la sortie
sous la forme
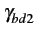 (f )= (f )= 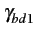 (f ) (f ) T=T0G(f )+ T=T0G(f )+ 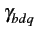 (f )= (f )=  kBT0G(f )+ kBT0G(f )+ 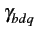 (f ) (f ) |
(3.19) |
Dès lors,
F0(f )= 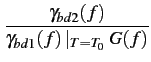 = 1 + = 1 + 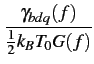 |
(3.20) |
Le facteur de bruit est évidemment supérieur ou égal à l'unité. Il
fait l'objet de mesure et caractérise le quadripôle.
Soient
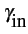 (f )
et
(f )
et
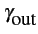 (f )
les densités
spectrales du signal utile respectivement à l'entrée et à la sortie
du quadripôle. Le rapport du signal à bruit à l'entrée vaut donc
(f )
les densités
spectrales du signal utile respectivement à l'entrée et à la sortie
du quadripôle. Le rapport du signal à bruit à l'entrée vaut donc
Pareillement, à la sortie du quadripôle,
Dès lors,
Mais, comme le signal est amplifié par un gain G(f )
, c'est-à-dire
que
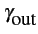 (f )= G(f )
(f )= G(f )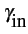 (f )
, ce rapport devient
(f )
, ce rapport devient
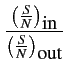 = = 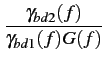 = F0(f ) = F0(f ) |
(3.24) |
En d'autres termes, le facteur de bruit n'est jamais que le quotient
du rapport signal à bruit en entrée par le rapport signal à bruit
en sortie. Il représente donc la dégradation du rapport signal à bruit,
après passage dans un quadripôle.
À partir du facteur de bruit, on peut aussi calculer la puissance
de bruit disponible en sortie
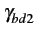 (f )= (f )= 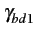 (f ) (f ) T=T0G(f )F0(f ) T=T0G(f )F0(f ) |
(3.25) |
Cette formulation permet d'exprimer le bruit injecté par le quadripôle
par un bruit équivalent qui serait placé à l'entrée. Le dessin de
la figure 3.5 montre les deux circuits
équivalents.
Figure 3.5:
Un quadripôle bruité et son schéma équivalent.
|
|
Le facteur de bruit traduit la dégradation du rapport signal à bruit
en sortie du quadripôle. Comme il dépend de la fréquence, on lui préfère
parfois le facteur de bruit moyen.
Définition 21
Le facteur de bruit moyen
est le rapport de (1) la puissance de bruit disponible à la sortie
du quadripôle à (2) la partie de cette puissance due au dipôle générateur
supposé à la température de bruit
T0 = 290 [K]
.
Par définition du facteur de bruit ponctuel, la puissance de bruit
disponible à la sortie du quadripôle possède une densité spectrale
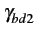 (f )= (f )=  kBT0G(f )F0(f ) kBT0G(f )F0(f ) |
(3.26) |
on a alors l'expression du facteur de bruit moyen
F0m = 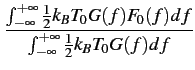 = = 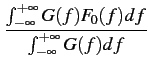 |
(3.27) |
Il s'agit d'une grandeur qui n'est pas normalisée, contrairement au
facteur de bruit.
Si la température de bruit du dipôle était
Ts 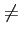 T0
, on
pourrait définir un facteur de bruit F(f )
, en reprenant point par
point le raisonnement précédent. En égalant la densité spectrale de
bruit propre au quadripôle
T0
, on
pourrait définir un facteur de bruit F(f )
, en reprenant point par
point le raisonnement précédent. En égalant la densité spectrale de
bruit propre au quadripôle
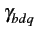 (f ) (f ) |
= |
(F0(f )- 1) kBT0G(f ) kBT0G(f ) |
(3.28) |
| |
= |
(F(f )- 1) kBTsG(f ) kBTsG(f ) |
(3.29) |
Comme le gain n'est a priori pas fonction de la température, pour
toute fréquence f
,
| (F - 1)Ts = (F0 -1)T0 |
(3.30) |
d'où
F = 1 + 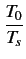 (F0 - 1) (F0 - 1) |
(3.31) |
et une relation identique entre F0m
et Fm
. F
, appelé
facteur de mérite, exprime la dégradation
du rapport signal à bruit lorsque la température du dipôle générateur
est Ts
.
Marc Van Droogenbroeck. Tous droits réservés.
2007-10-27
![]() (f )=
(f )= ![]() (f )
(f )![]() T=T0G(f )+
T=T0G(f )+ ![]() (f )=
(f )= ![]() kBT0G(f )+
kBT0G(f )+ ![]() (f )
(f )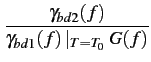 = 1 +
= 1 + 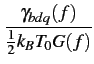
![]() (f )
(f )
![]() (f )
(f )
![]()
![]()
![]() =
= 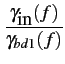
![]()
![]()
![]() =
= 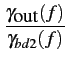
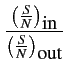 =
= 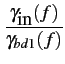
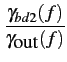
![]() (f )= G(f )
(f )= G(f )![]() (f )
(f )
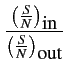 =
= 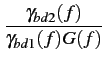 = F0(f )
= F0(f )![]() (f )=
(f )= ![]() (f )
(f )![]() T=T0G(f )F0(f )
T=T0G(f )F0(f )![]() (f )=
(f )= ![]() kBT0G(f )F0(f )
kBT0G(f )F0(f )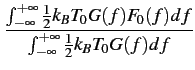 =
= 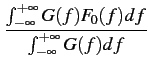
![]() T0
T0
![]() (f )
(f )![]() kBT0G(f )
kBT0G(f )![]() kBTsG(f )
kBTsG(f )![]() (F0 - 1)
(F0 - 1)