Les modulations linéaires classiques sont telles que
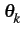 = 2
= 2 fckT
.
Dès lors, le signal modulé prend la forme
fckT
.
Dès lors, le signal modulé prend la forme
s(t) = Re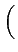 es(t) ej es(t) ej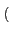 2 2 fct + fct + 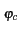 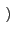 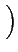 |
(4.6) |
où l'enveloppe complexe s'exprime par
| es(t) |
= |
 dk(t) dk(t) |
(4.7) |
| |
= |
 Dk gk(t - kT) Dk gk(t - kT) |
(4.8) |
Le signal gk(t)
est un signal de mise en forme réel (non complexe).
Pour la simplicité, nous choisirons une onde de mise en forme unique
gk(t) = g(t), 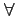 k
. Dk
est une variable aléatoire
complexe qui contient l'information numérique à transmettre. Elle
prendra généralement la forme
Dk = Ak + jBk
où Ak
et
Bk
sont deux variables aléatoires réelles.
k
. Dk
est une variable aléatoire
complexe qui contient l'information numérique à transmettre. Elle
prendra généralement la forme
Dk = Ak + jBk
où Ak
et
Bk
sont deux variables aléatoires réelles.
L'enveloppe complexe s'exprime également par
es(t) = sI(t) + jsQ(t)
où les signaux réels sI(t)
et sQ(t)
représentent respectivement
la composante en phase et en quadrature
| sI(t) |
= |
 Ak g(t - kT) Ak g(t - kT) |
(4.9) |
| sQ(t) |
= |
 Bk g(t - kT) Bk g(t - kT) |
(4.10) |
ce qui conduit à l'expression suivante du signal modulé
s(t) = sI(t) cos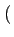 2 2 fct + fct + 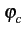  - sQ(t) sin - sQ(t) sin 2 2 fct + fct + 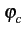 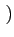 |
(4.11) |
soit encore, en remplaçant sI
et sQ
par leur valeur,
s(t) = 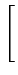  Ak g(t - kT) Ak g(t - kT)![$\displaystyle \left.\vphantom{\sum_{k=-\infty}^{+\infty}A_{k} g(t-kT)}\right]$](img519.gif) cos cos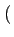 2 2 fct + fct + 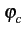 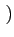 - - 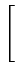  Bk g(t - kT) Bk g(t - kT)![$\displaystyle \left.\vphantom{\sum_{k=-\infty}^{+\infty}B_{k} g(t-kT)}\right]$](img521.gif) sin sin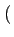 2 2 fct + fct + 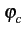 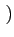 |
(4.12) |
En toute généralité donc, le signal modulé peut être vu comme la modulation
en quadrature de deux signaux numériques en bande de base (de type
NRZ).
Marc Van Droogenbroeck. Tous droits réservés.
2007-10-27
![]() k
k
![]() Ak g(t - kT)
Ak g(t - kT)![]() Bk g(t - kT)
Bk g(t - kT)![]() 2
2![]() fct +
fct + ![]()
![]() - sQ(t) sin
- sQ(t) sin![]() 2
2![]() fct +
fct + ![]()
![]()
![]()
![]() Ak g(t - kT)
Ak g(t - kT)![]() cos
cos![]() 2
2![]() fct +
fct + ![]()
![]() -
- ![]()
![]() Bk g(t - kT)
Bk g(t - kT)![]() sin
sin![]() 2
2![]() fct +
fct + ![]()
![]()