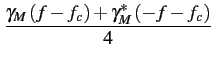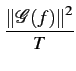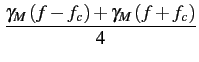Sous-sections
Le calcul de la densité spectrale de puissance d'un processus stochastique
n'a véritablement de sens que si ce processus est stationnaire au
sens large. Pour rappel un processus aléatoire X(t)
est stationnaire
au sens large si les deux conditions suivantes sont remplies
- sa moyenne
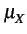 est indépendante du temps t
,
est indépendante du temps t
,
- sa fonction d'autocorrélation
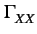
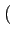 t, t -
t, t - 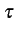
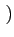 = E
= E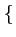 X(t)X * (t -
X(t)X * (t - 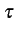 )
)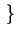 ne dépend que de la différence de temps
ne dépend que de la différence de temps 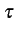 entre les instants
d'observation. La fonction d'autocorrélation est alors notée
entre les instants
d'observation. La fonction d'autocorrélation est alors notée
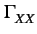
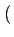
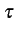
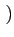 .
.
La densité spectrale de puissance d'un processus stochastique stationnaire
au sens large s'obtient en calculant la transformée de FOURIER
de sa fonction d'autocorrélation.
Le signal numérique modulé est un processus stochastique S(t)
que
l'on peut écrire, en prenant arbitrairement
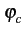 = 0
, sous
la forme
= 0
, sous
la forme
S(t) = Re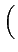 M(t) ej2 M(t) ej2 fct fct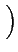 |
(4.13) |
où M(t)
est un processus stochastique complexe. Remarquons tout
d'abord que le processus stochastique S(t)
n'est pas stationnaire
au sens large vu car sa moyenne dépend du temps. Il est donc nécessaire
de stationnariser le signal. Pour cela, nous ajoutons une phase aléatoire
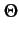 uniformément répartie sur
uniformément répartie sur
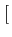 0, 2
0, 2
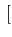
S(t) = Re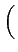 M(t) ej M(t) ej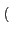 2 2 fct + fct + 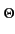 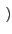 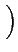 |
(4.14) |
Comme le processus stochastique M(t)
et la variable aléatoire 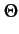 sont non-corrélés, il est aisé de montrer que la moyenne du processus
stochastique S(t)
est nulle et donc indépendante du temps.
sont non-corrélés, il est aisé de montrer que la moyenne du processus
stochastique S(t)
est nulle et donc indépendante du temps.
Déterminons la fonction d'autocorrélation du signal modulé
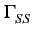 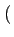 t, t - t, t - 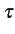  |
= |
E S(t) S * (t - S(t) S * (t - 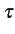 ) ) |
(4.15) |
| |
= |
E S(t) S(t - S(t) S(t - 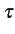 ) ) |
(4.16) |
où nous avons utilisé le fait que le signal modulé est réel. Comme
S(t) =   M(t) ej M(t) ej 2 2 fct + fct +   + M * (t) e-j + M * (t) e-j 2 2 fct + fct +   ![% latex2html id marker 28340
$\displaystyle \left.\vphantom{M(t) e^{j\left(2\...
...}t+\Theta\right)}+{M}^{\ast}(t) e^{-j\left(2\pi f_{c}t+\Theta\right)}}\right]$](img551.gif) |
(4.17) |
et, en remplaçant S(t)
par sa valeur, le calcul des espérances
fournit4.1
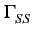  t, t - t, t - 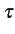 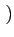 |
= |
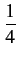 E E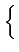 M(t) M * (t - M(t) M * (t - 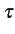 ) ej2 ) ej2 fc fc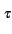 + M * (t) M(t - + M * (t) M(t - 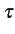 ) e-j2 ) e-j2 fc fc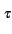  |
(4.18) |
| |
= |
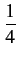 E E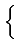 2 Re 2 Re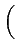 M(t) M * (t - M(t) M * (t - 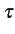 ) ej2 ) ej2 fc fc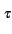   |
(4.19) |
| |
= |
 Re Re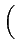 E E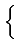 M(t) M * (t - M(t) M * (t - 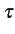 ) ej2 ) ej2 fc fc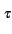 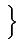 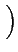 |
(4.20) |
| |
= |
 Re Re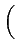 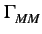 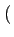 t, t - t, t - 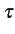 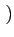 ej2 ej2 fc fc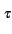 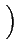 |
(4.21) |
Dès lors, il vient que, si l'enveloppe complexe M(t)
est un processus
stochastique stationnaire au sens large, le signal modulé S(t)
est également stationnaire au sens large. Il est alors possible de
calculer sa densité spectrale de puissance en prenant la transformée
de FOURIER de sa fonction d'autocorrélation. Étant donné que
il vient finalement
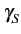 (f )= (f )= 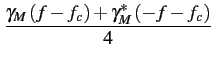 |
(4.23) |
où
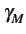 (f )
est la densité spectrale de puissance de l'enveloppe
complexe M(t)
.
(f )
est la densité spectrale de puissance de l'enveloppe
complexe M(t)
.
L'enveloppe complexe du signal modulé est un processus stochastique
complexe exprimé par
M(t) =  Dk g(t - kT) Dk g(t - kT) |
(4.24) |
La séquence de variables aléatoires Dk
est caractérisée par
- sa moyenne:
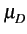 = E
= E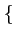 Dk
Dk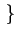
- sa variance:
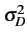 = E
= E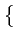
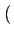 Dk -
Dk - 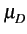
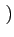
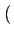 Dk -
Dk - 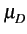
- sa fonction d'autocorrélation:
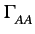
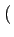 k, k - l
k, k - l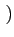 = E
= E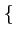 DkDk-l *
DkDk-l * 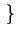
- sa fonction d'autocovariance:
CAA(k, k - l )= E
 Dk -
Dk - 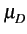
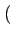 Dk-l -
Dk-l - 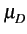
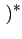
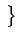
Après stationnarisation de la séquence de variables aléatoires Dk
,
on montre (voir cours de ``Principes des télécommunications analogiques
et numériques'') que la densité spectrale de puissance de M(t)
est donnée par
où
Si on ajoute l'hypothèse de variables aléatoires Dk
non-corrélées4.2 (
CDD(k, k - l )= 0
), on montre que
La densité spectrale de puissance de l'enveloppe complexe M(t)
est donc réelle et symétrique.
En conséquence des relations 4.23 et 4.27,
la densité spectrale de puissance du signal modulé est fournie par
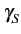 (f )= (f )= 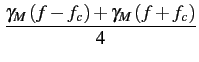 |
(4.28) |
La seule connaissance de l'enveloppe complexe et de la fréquence porteuse
permet donc de déterminer la densité spectrale d'un signal numérique
classique.
Notes
- ...
fournit4.1
- En fait, l'espérance des deux termes faisant intervenir la variable
aléatoire
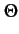 est nulle.
est nulle.
- ... non-corrélées4.2
- La non-corrélation des symboles successifs garantit un transfert d'information
maximum. Mais en contrepartie de l'absence de redondance, l'information
est très sensible à des effets de bruit.
Marc Van Droogenbroeck. Tous droits réservés.
2007-10-27
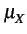
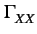
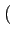 t, t -
t, t - 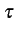
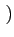 = E
= E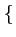 X(t)X * (t -
X(t)X * (t - 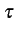 )
)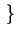
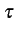
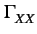
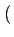
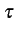
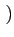
![]() = 0
= 0
![]() M(t) ej2
M(t) ej2![]() fct
fct![]()
![]()
![]() 0, 2
0, 2![]()
![]()
![]() M(t) ej
M(t) ej![]() 2
2![]() fct +
fct + ![]()
![]()
![]()
![]()
![]()
![]() t, t -
t, t - ![]()
![]()
![]() S(t) S * (t -
S(t) S * (t - ![]() )
)![]()
![]() S(t) S(t -
S(t) S(t - ![]() )
)![]()
![]()
![]() M(t) ej
M(t) ej![]() 2
2![]() fct +
fct + ![]()
![]() + M * (t) e-j
+ M * (t) e-j![]() 2
2![]() fct +
fct + ![]()
![]()
![]()
![]()
![]() t, t -
t, t - ![]()
![]()
![]() E
E![]() M(t) M * (t -
M(t) M * (t - ![]() ) ej2
) ej2![]() fc
fc![]() + M * (t) M(t -
+ M * (t) M(t - ![]() ) e-j2
) e-j2![]() fc
fc![]()
![]()
![]() E
E![]() 2 Re
2 Re![]() M(t) M * (t -
M(t) M * (t - ![]() ) ej2
) ej2![]() fc
fc![]()
![]()
![]()
![]() Re
Re![]() E
E![]() M(t) M * (t -
M(t) M * (t - ![]() ) ej2
) ej2![]() fc
fc![]()
![]()
![]()
![]() Re
Re![]()
![]()
![]() t, t -
t, t - ![]()
![]() ej2
ej2![]() fc
fc![]()
![]()
![]()
![]()
![]()
![]() =
= ![]()
![]()
![]()
![]()
![]()
![]() ej2
ej2![]() fc
fc![]() +
+ ![]()
![]()
![]()
![]() e-j2
e-j2![]() fc
fc![]()
![]()
![]() (f )
(f )
![]() = E
= E![]() Dk
Dk![]()
![]() = E
= E![]()
![]() Dk -
Dk - ![]()
![]()
![]() Dk -
Dk - ![]()
![]()
![]()
![]()
![]() k, k - l
k, k - l![]() = E
= E![]() DkDk-l *
DkDk-l * ![]()
![]()
![]() Dk -
Dk - ![]()
![]()
![]() Dk-l -
Dk-l - ![]()
![]()
![]()
![]() (f )=
(f )= ![]()
![]() (f )
(f )![]()
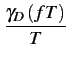
![]()
![]() fT
fT![]() =
= ![]()
![]()
![]() l
l![]() e-j2
e-j2![]() lfT
lfT![]()