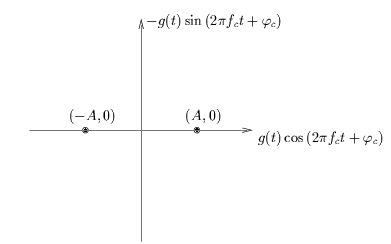).
L'enveloppe complexe d'un signal modulé ASK, qui vaut
es(t) =  Ak g(t - kT) Ak g(t - kT) |
(4.29) |
est donc purement réelle.
Il est courant de choisir comme signal de mise en forme une impulsion
rectangulaire de durée T
g(t) = rect[0, T]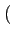 t t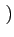 |
(4.30) |
Pour arriver à interpréter le signal modulé, on détermine l'enveloppe
a(t)
et la phase
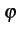 (t)
du signal modulé. Ces deux signaux
s'obtiennent aisément à partir de l'enveloppe complexe par la relation
(t)
du signal modulé. Ces deux signaux
s'obtiennent aisément à partir de l'enveloppe complexe par la relation
es(t) = a(t) ej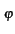 (t) (t) |
(4.31) |
Étant donné que la variable aléatoire Ak
peut s'écrire
Ak = 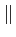 Ak
Ak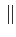 e
e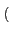 1 - sgn
1 - sgn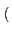 Ak
Ak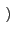
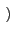
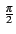 j
,
nous pouvons déduire
j
,
nous pouvons déduire
| a(t) |
= |
 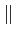 Ak Ak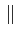 rect[0, T] rect[0, T]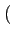 t - kT t - kT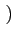 |
(4.32) |
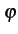 (t) (t) |
= |
 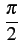 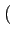 1 - sgn 1 - sgn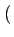 Ak Ak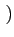 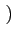 rect[0, T] rect[0, T]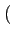 t - kT t - kT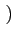 |
(4.33) |
Il apparaît que l'enveloppe du signal varie par paliers, ce qui
est un inconvénient si le signal passe au travers d'un canal affectant
l'amplitude ou d'un système non-linéaire, comme par exemple un amplificateur
travaillant à saturation. Quant à la phase, elle marque des discontinuités
par sauts de  . Ces sauts de phase sont également critiques car
il nécessite des filtres de réception à large bande passante sous
peine de détériorer le signal modulé.
. Ces sauts de phase sont également critiques car
il nécessite des filtres de réception à large bande passante sous
peine de détériorer le signal modulé.
Dans le cas de la modulation ASK-2, la variable aléatoire
Ak
peut prendre deux valeurs: + A
ou - A
. Pour cette modulation,
on voit que l'enveloppe du signal est constante. Par contre, la phase
subit toujours des sauts de  radians toutes les T
secondes.
radians toutes les T
secondes.
Il est courant de représenter une modulation par un diagramme
de constellations ou diagramme des états
de phase, qui n'est rien d'autre
que le plan complexe de la variable aléatoire complexe Dk
, dans
lequel on représente toutes les valeurs que peut prendre Dk
.
On attribue le signal
g(t)cos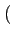 2
2 fct +
fct + 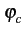
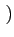 ,
correspondant à Ak
, à l'axe réel pour faire référence à la composante
en phase et
- g(t)sin
,
correspondant à Ak
, à l'axe réel pour faire référence à la composante
en phase et
- g(t)sin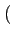 2
2 fct +
fct + 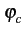
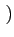 , correspondant
à Bk
, à l'axe imaginaire pour faire référence à la composante
en quadrature.
, correspondant
à Bk
, à l'axe imaginaire pour faire référence à la composante
en quadrature.
La présence de g(t)
signifie que le diagramme de constellations
est indépendant du signal de mise en forme. La figure 4.1
montre le diagramme de constellations pour la modulation ASK-2.
Figure 4.1:
Diagramme des états de phase de la modulation ASK-2 ou BPSK.
|
|
Déterminons à présent la densité spectrale de puissance du signal
modulé ASK-2. Commençons par déterminer la densité spectrale de puissance
de l'enveloppe complexe. Nous ferons l'hypothèse que les deux amplitudes
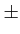 A
sont équiprobables. La moyenne
A
sont équiprobables. La moyenne 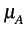 de la variable
aléatoire Ak
est donc nulle. Sa variance est donnée par
de la variable
aléatoire Ak
est donc nulle. Sa variance est donnée par
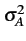 = E
= E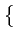 Ak2
Ak2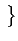 = A2
.
Le signal de mise en forme étant la fonction
rect[0, T]
= A2
.
Le signal de mise en forme étant la fonction
rect[0, T]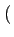 t
t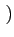 ,
sa transformée de FOURIER vaut
,
sa transformée de FOURIER vaut
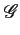 (f )= e-j2 (f )= e-j2 f f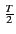 T sinc(fT) T sinc(fT) |
(4.34) |
Il en résulte une densité spectrale de puissance pour l'enveloppe
complexe donnée par
et finalement une densité spectrale de puissance du signal modulé
valant
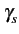 (f )= (f )= 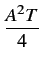 ![$\displaystyle \left\{\vphantom{ sinc^{2}\left[\left(f-f_{c}\right)T\right]+sinc^{2}\left[\left(f+f_{c}\right)T\right]}\right.$](img637.gif) sinc2 sinc2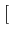 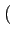 f - fc f - fc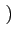 T T![$\displaystyle \left.\vphantom{\left(f-f_{c}\right)T}\right]$](img641.gif) + sinc2 + sinc2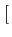 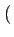 f + fc f + fc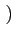 T T![$\displaystyle \left.\vphantom{\left(f+f_{c}\right)T}\right]$](img645.gif) ![$\displaystyle \left.\vphantom{ sinc^{2}\left[\left(f-f_{c}\right)T\right]+sinc^{2}\left[\left(f+f_{c}\right)T\right]}\right\}$](img646.gif) |
(4.36) |
Comme la variable aléatoire Ak
ne peut prendre que deux valeurs
dans le cas de la modulation ASK-2, le signal modulé ne transmet qu'un
seul bit d'information pendant la durée T
. Il vient donc que la
densité spectrale de puissance d'un signal ASK-2 est donnée par la
relation 4.36 pour T = Tb
où
Rb = 1/Tb
est
le débit binaire, encore appelé fréquence bit, exprimé en [b/s]
.
Marc Van Droogenbroeck. Tous droits réservés.
2007-10-27
![]() t
t![]()
![]() (t)
(t)
![]() (t)
(t)![]() Ak
Ak![]() e
e![]() 1 - sgn
1 - sgn![]() Ak
Ak![]()
![]()
![]() j
j
![]()
![]() Ak
Ak![]() rect[0, T]
rect[0, T]![]() t - kT
t - kT![]()
![]() (t)
(t)![]()
![]()
![]() 1 - sgn
1 - sgn![]() Ak
Ak![]()
![]() rect[0, T]
rect[0, T]![]() t - kT
t - kT![]()
![]()
![]()
![]() 2
2![]() fct +
fct + ![]()
![]()
![]() 2
2![]() fct +
fct + ![]()
![]()
![]() A
A
![]()
![]() = E
= E![]() Ak2
Ak2![]() = A2
= A2
![]() t
t![]()
![]() (f )= e-j2
(f )= e-j2![]() f
f![]() T sinc(fT)
T sinc(fT)![]() (f )= A2T sinc2
(f )= A2T sinc2![]() fT
fT![]()