Sous-sections
La modulation en quadrature de phase (QPSK) correspond
à une modulation PSK-4, c'est donc une modulation à 4 états (M = 4
).
La phase 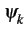 peut prendre les valeurs
peut prendre les valeurs
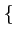 -3
-3 /4, -
/4, -  /4, +
/4, +  /4, +3
/4, +3 /4
/4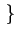 .
Autrement dit, la variable aléatoire Dk
prend une des valeurs
suivantes4.3
.
Autrement dit, la variable aléatoire Dk
prend une des valeurs
suivantes4.3
Dk 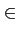 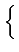 Ae-j Ae-j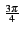 , Ae-j , Ae-j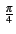 , Aej , Aej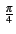 , Aej , Aej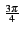 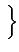 |
(4.48) |
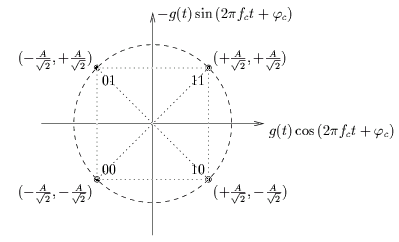
Le diagramme de constellations est représenté à la figure 4.2.
Figure 4.2:
Diagramme de constellations pour la modulation QPSK.
|
|
Considérons une source binaire fournissant le train d'impulsions suivant
I(t) =  Ik Ik 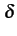 (t - kTb) (t - kTb) |
(4.49) |
où Ik = + 1
correspond à l'information binaire 1 et Ik = - 1
correspond à l'information binaire 0. Le débit binaire est égal à
Rb = 1/Tb
. À partir de la séquence I(t)
, nous formons les
deux séquences
| sI(t) |
= |
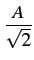  I2k g(t - kT) = I2k g(t - kT) =  Ak g(t - kT) Ak g(t - kT) |
(4.50) |
| sQ(t) |
= |
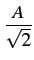  I2k+1 g(t - kT) = I2k+1 g(t - kT) =  Bk g(t - kT) Bk g(t - kT) |
(4.51) |
où T = 2Tb
, g(t)
est une impulsion de mise en forme de durée
T
,
Ak = I2k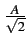 et
Bk = I2k+1
et
Bk = I2k+1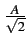 .
Ces deux séquences correspondent respectivement aux bits pairs et
impairs de la séquence de départ et constituent les composantes en
phase sI(t)
et en quadrature sQ(t)
du signal modulé QPSK.
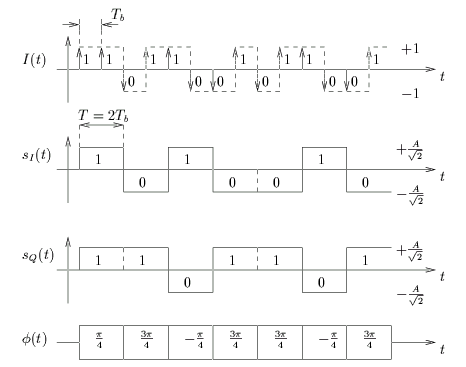
La figure 4.3 illustre la formation de ces séquences
pour un signal de mise en forme égal à
.
Ces deux séquences correspondent respectivement aux bits pairs et
impairs de la séquence de départ et constituent les composantes en
phase sI(t)
et en quadrature sQ(t)
du signal modulé QPSK.
La figure 4.3 illustre la formation de ces séquences
pour un signal de mise en forme égal à
g(t) = rect[0, T]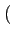 t t = rect[0, 2Tb] = rect[0, 2Tb]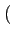 t t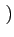 |
(4.52) |
qui correspond à la modulation QPSK classique.
Figure 4.3:
Formation des composantes en phase et en quadrature pour la modulation
QPSK (avec mise en forme par un signal rectangulaire).
|
|
Nous allons à présent déterminer l'enveloppe et la phase instantanée
pour une impulsion de mise en forme rectangulaire. L'enveloppe complexe
est donnée par
| es(t) |
= |
sI(t) + j sQ(t) |
(4.53) |
| |
= |
 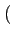 Ak + j Bk Ak + j Bk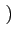 rect[0, T] rect[0, T]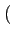 t - kT t - kT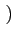 |
(4.54) |
| |
= |
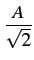  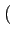 I2k + j I2k+1 I2k + j I2k+1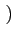 rect[0, T] rect[0, T]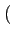 t - kT t - kT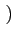 |
(4.55) |
Il vient alors
| a(t) |
= |
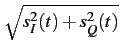 |
(4.56) |
| |
= |
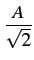  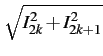 rect[0, T] rect[0, T]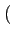 t - kT t - kT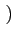 |
(4.57) |
| |
= |
A  rect[0, T] rect[0, T]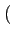 t - kT t - kT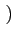 |
(4.58) |
et
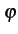 (t) = (t) =  rect[0, T] rect[0, T]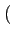 t - kT t - kT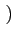 tan-1 tan-1 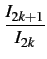 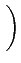 |
(4.59) |
Nous voyons donc que l'enveloppe du signal modulé est constante et
égale à A
. Le rapport
I2k+1/I2k
peut prendre les valeurs
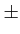 1
, ce qui correspondrait à 2 états seulement. Cependant, la
fonction tan-1
est définie à
1
, ce qui correspondrait à 2 états seulement. Cependant, la
fonction tan-1
est définie à  radians près. En fait,
pour déterminer la phase, il faut se référer au plan de constellations
(figure 4.2).
radians près. En fait,
pour déterminer la phase, il faut se référer au plan de constellations
(figure 4.2).
La phase varie donc par paliers de manière discontinue. La figure 4.3
montre la valeur instantanée de
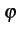 (t)
pour une séquence binaire
donnée. On peut remarquer que la phase peut subir des sauts de
(t)
pour une séquence binaire
donnée. On peut remarquer que la phase peut subir des sauts de
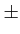
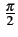 ou de
ou de 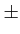
 toutes les T
secondes. Ces différentes transitions
sont représentées en pointillés sur la figure 4.2.
Lors des transitions
toutes les T
secondes. Ces différentes transitions
sont représentées en pointillés sur la figure 4.2.
Lors des transitions 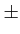
 , on voit que l'enveloppe instantanée
du signal peut s'annuler pendant le temps de la transition (passage
par zéro dans le plan des constellations). En effet, des transitions
instantanées sont irréalisables physiquement. Si le signal est filtré,
il peut perdre sa propriété d'enveloppe constante, ce qui est gênant
lorsque qu'il passe dans un système présentant des distorsions d'amplitude.
Enfin, des sauts brusques de phase impliquent également une bande
passante plus importante. La figure 4.4 montre un signal
modulé QPSK pour une séquence binaire donnée.
, on voit que l'enveloppe instantanée
du signal peut s'annuler pendant le temps de la transition (passage
par zéro dans le plan des constellations). En effet, des transitions
instantanées sont irréalisables physiquement. Si le signal est filtré,
il peut perdre sa propriété d'enveloppe constante, ce qui est gênant
lorsque qu'il passe dans un système présentant des distorsions d'amplitude.
Enfin, des sauts brusques de phase impliquent également une bande
passante plus importante. La figure 4.4 montre un signal
modulé QPSK pour une séquence binaire donnée.
Figure:
Illustration de la modulation QPSK: (a) séquence binaire I(t)
,
(b) signal sI(t)
, (c) signal sQ(t)
, (d)
sI(t) cos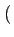 2
2 fct
fct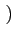 ,
(e)
sQ(t) sin
,
(e)
sQ(t) sin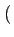 2
2 fct
fct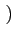 et (f) signal modulé
s(t)
.
et (f) signal modulé
s(t)
.
|
|
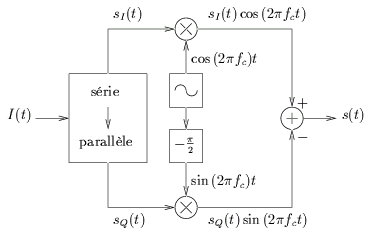
La figure 4.5 montre le modulateur QPSK. Les
différents signaux apparaissant sur cette figure sont également présents
à la figure 4.4.
Figure 4.5:
Modulateur QPSK.
|
|
Le signal modulé QPSK correspond à la modulation en quadrature de
deux signaux numériques en bande de base. La première phase de la
démodulation consiste donc à retrouver les composantes en phase et
en quadrature du signal modulé. Les deux signaux numériques en bande
de base obtenus sont ensuite démodulés grâce au filtre adapté (un
pour chaque signal) et recombinés pour former la séquence binaire
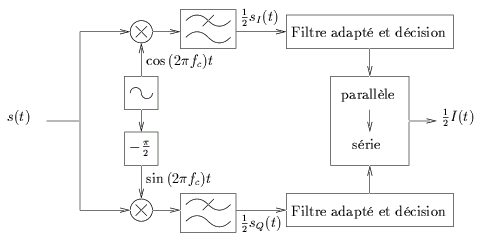
de départ. Le schéma du démodulateur QPSK est repris à la figure 4.6.
Figure 4.6:
Démodulateur QPSK.
|
|
L'enveloppe complexe du signal modulé est donnée par
es(t) =  Dk g(t - kT) Dk g(t - kT) |
(4.60) |
où le signal de mise en forme g(t)
et la variable aléatoire Dk
valent respectivement
| g(t) |
= |
rect[0, 2Tb]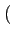 t t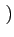 |
(4.61) |
| Dk |
= |
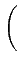 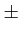 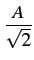 , ,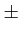 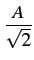 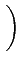 |
(4.62) |
Nous faisons à nouveau l'hypothèse que les quatre valeurs possibles
pour Dk
sont équiprobables. La moyenne 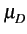 est donc nulle
et la variance est égale à
est donc nulle
et la variance est égale à
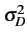 = E
= E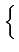
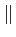 Dk
Dk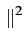
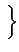 = A2
.
Il vient, après calcul de la transformée de FOURIER du signal
de mise en forme,
= A2
.
Il vient, après calcul de la transformée de FOURIER du signal
de mise en forme,
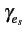 (f )= 2A2Tb sinc2 (f )= 2A2Tb sinc2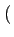 2fTb 2fTb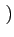 |
(4.63) |
La densité spectrale de puissance d'un signal modulé en QPSK s'exprime
finalement par
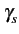 (f )= (f )= 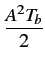 ![$\displaystyle \left\{\vphantom{ sinc^{2}\left[\left(f-f_{c}\right)2T_{b}\right]+sinc^{2}\left[\left(f+f_{c}\right)2T_{b}\right]}\right.$](img715.gif) sinc2 sinc2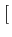 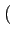 f - fc f - fc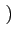 2Tb 2Tb![$\displaystyle \left.\vphantom{\left(f-f_{c}\right)2T_{b}}\right]$](img717.gif) + sinc2 + sinc2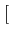 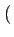 f + fc f + fc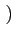 2Tb 2Tb![$\displaystyle \left.\vphantom{\left(f+f_{c}\right)2T_{b}}\right]$](img719.gif) ![$\displaystyle \left.\vphantom{ sinc^{2}\left[\left(f-f_{c}\right)2T_{b}\right]+sinc^{2}\left[\left(f+f_{c}\right)2T_{b}\right]}\right\}$](img720.gif) |
(4.64) |
et est identique à celle de la modulation BPSK pour un débit binaire
double.
Notes
- ...
suivantes4.3
- On utilise parfois l'ensemble de ces valeurs décalées de
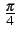 ,
ce qui conduit à l'ensemble des phases possibles suivant:
,
ce qui conduit à l'ensemble des phases possibles suivant:
 - A, Ae-j
- A, Ae-j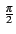 , A, Aej
, A, Aej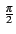
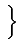 .
.
Marc Van Droogenbroeck. Tous droits réservés.
2007-10-27
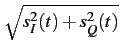
 rect[0, T]
rect[0, T]![]() (t)
(t)
![]()
![]()
![]()
![]()
![]()
![]()
![]() 2
2![]() fct
fct![]()
![]() 2
2![]() fct
fct![]()
![\includegraphics[width=13cm]{images/qpsk}](img704.gif)
![]() Dk g(t - kT)
Dk g(t - kT)![]() t
t![]()
![]()
![]()
![]() ,
,![]()
![]()
![]()
![]()
![]() = E
= E![]()
![]() Dk
Dk![]()
![]() = A2
= A2
![]() (f )= 2A2Tb sinc2
(f )= 2A2Tb sinc2![]() 2fTb
2fTb![]()
![]()
![]() - A, Ae-j
- A, Ae-j![]() , A, Aej
, A, Aej![]()
![]()