Les modulations linéaires à décalage présentent la particularité que
la variable aléatoire Dk
est purement réelle (
Dk = Ak
)
et que la phase
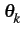 de l'expression (4.5)
est égale à
2
de l'expression (4.5)
est égale à
2 fckT + k
fckT + k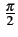 . L'expression de l'enveloppe
complexe du signal modulé se simplifie donc en
. L'expression de l'enveloppe
complexe du signal modulé se simplifie donc en
es(t) =  Ak g(t - kT) ejk Ak g(t - kT) ejk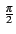 |
(4.65) |
Bien que la variable aléatoire Ak
soit réelle, l'enveloppe complexe
es(t)
est bel et bien un signal à valeurs complexes.
Mettons-nous à présent dans le vas où T = Tb
, la durée de l'impulsion
de mise en forme g(t)
n'étant pas encore fixée. Le signal modulé
prend la forme
| s(t) |
= |
 Ak g(t - kTb) cos Ak g(t - kTb) cos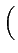 2 2 fct + fct + 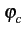 + k + k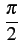  |
(4.66) |
| |
= |
  Ak g(t - kTb) cos Ak g(t - kTb) cos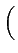 k k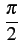 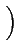 ![$\displaystyle \left.\vphantom{\sum_{k=-\infty}^{+\infty}A_{k} g(t-kT_{b}) \cos\left(k\frac{\pi}{2}\right)}\right]$](img726.gif) cos cos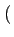 2 2 fct + fct + 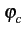  |
(4.67) |
| |
|
-   Ak g(t - kTb) sin Ak g(t - kTb) sin k k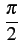 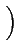 ![$\displaystyle \left.\vphantom{\sum_{k=-\infty}^{+\infty}A_{k} g(t-kT_{b}) \sin\left(k\frac{\pi}{2}\right)}\right]$](img728.gif) sin sin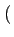 2 2 fct + fct + 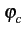 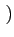 |
(4.68) |
En tenant compte du fait que
cos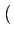 k
k /2
/2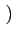 = 0
pour k
impair et que
sin
= 0
pour k
impair et que
sin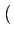 k
k /2
/2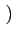 = 0
pour k
pair, les composantes
en phase et en quadrature peuvent s'exprimer par
= 0
pour k
pair, les composantes
en phase et en quadrature peuvent s'exprimer par
| sI(t) |
= |
 Ak g(t - kTb) cos Ak g(t - kTb) cos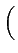 k k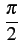  |
(4.69) |
| |
= |
 A2k A2k 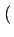 -1 -1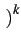 g g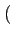 t - 2kTb t - 2kTb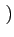 |
(4.70) |
et
| sQ(t) |
= |
 Ak g(t - kTb) sin Ak g(t - kTb) sin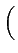 k k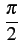 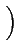 |
(4.71) |
| |
= |
 A2k+1 A2k+1 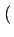 -1 -1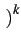 g g t - t - 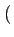 2k + 1 2k + 1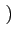 Tb Tb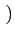 |
(4.72) |
On voit que, par rapport aux modulations linéaires classiques, les
séquences sI(t)
et sQ(t)
sont décalées entre elles de
la durée d'un bit Tb
, d'où le nom de modulation à décalage.
Marc Van Droogenbroeck. Tous droits réservés.
2007-10-27
![]() Ak g(t - kTb) cos
Ak g(t - kTb) cos![]() 2
2![]() fct +
fct + ![]() + k
+ k![]()
![]()
![]()
![]() Ak g(t - kTb) cos
Ak g(t - kTb) cos![]() k
k![]()
![]()
![]() cos
cos![]() 2
2![]() fct +
fct + ![]()
![]()
![]()
![]() Ak g(t - kTb) sin
Ak g(t - kTb) sin![]() k
k![]()
![]()
![]() sin
sin![]() 2
2![]() fct +
fct + ![]()
![]()
![]() k
k![]() /2
/2![]() = 0
= 0
![]() k
k![]() /2
/2![]() = 0
= 0
![]() Ak g(t - kTb) cos
Ak g(t - kTb) cos![]() k
k![]()
![]()
![]() A2k
A2k ![]() -1
-1![]() g
g![]() t - 2kTb
t - 2kTb![]()
![]() Ak g(t - kTb) sin
Ak g(t - kTb) sin![]() k
k![]()
![]()
![]() A2k+1
A2k+1 ![]() -1
-1![]() g
g![]() t -
t - ![]() 2k + 1
2k + 1![]() Tb
Tb![]()