Sous-sections
Bien que plus avantageuse que la modulation QPSK, la modulation OQPSK
présente encore un inconvénient: des discontinuités de phase qui entraînent
une bande passante importante. La modulation à saut de phase minimum
(MSK) permet de supprimer ces discontinuités de phase. Celle-ci
présente les mêmes particularités que la modulation OQPSK sauf que
les sauts de phase se font de manière continue pendant la durée d'un
bit Tb
de telle sorte que la phase instantanée du signal modulé
est une fonction continue du temps.
La caractéristique qui différencie la modulation MSK de la modulation
OQPSK est le signal de mise en forme qui prend maintenant la forme
g(t) = rect[0, 2Tb]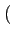 t t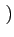 sin sin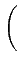 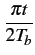 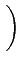 |
(4.95) |
Les séquences sI(t)
et sQ(t)
sont formées exactement de
la même manière que pour la modulation OQPSK. La composante en phase
sI(t)
s'écrit sous la forme
| sI(t) |
= |
A  I2k rect[0, 2Tb] I2k rect[0, 2Tb]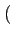 t - 2kTb t - 2kTb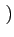 sin sin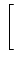  ![$\displaystyle \left.\vphantom{\frac{\pi\left(t-2kT_{b}\right)}{2T_{b}}}\right]$](img787.gif) |
(4.96) |
| |
= |
 A I2k A I2k 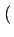 -1 -1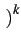 rect[0, 2Tb] rect[0, 2Tb]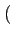 t - 2kTb t - 2kTb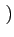 sin sin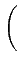 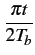 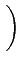 |
(4.97) |
| |
= |
cos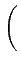 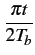 - - 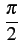 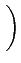  A2k rect[0, 2Tb] A2k rect[0, 2Tb]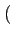 t - 2kTb t - 2kTb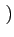 |
(4.98) |
où nous avons utilisé le fait que
sin(a) = cos(a - 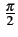 )
et défini
A2k = A I2k
)
et défini
A2k = A I2k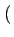 -1
-1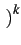 . Le signal sI(t)
peut être vu comme un signal du type NRZ multiplié par une cosinusoïde.
Un développement similaire donne pour la composante en quadrature
de phase
. Le signal sI(t)
peut être vu comme un signal du type NRZ multiplié par une cosinusoïde.
Un développement similaire donne pour la composante en quadrature
de phase
sQ(t) = sin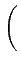 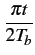 - - 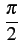 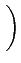  A2k+1 rect[0, 2Tb] A2k+1 rect[0, 2Tb]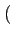 t - 2kTb t - 2kTb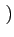 |
(4.99) |
où
A2k+1 = A I2k+1 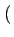 -1
-1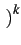 . Ces deux expressions
vont nous permettre de déterminer l'enveloppe instantanée et la variation
de phase instantanée du signal modulé. L'enveloppe est donnée par
. Ces deux expressions
vont nous permettre de déterminer l'enveloppe instantanée et la variation
de phase instantanée du signal modulé. L'enveloppe est donnée par
| a(t) |
= |
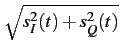 |
(4.100) |
| |
= |
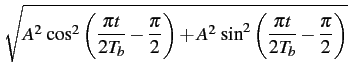 |
(4.101) |
| |
= |
A |
(4.102) |
L'enveloppe du signal modulé est donc constante et égale à A
. La
phase instantanée peut s'exprimer par
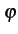 (t) (t) |
= |
tan-1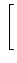 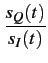 ![$\displaystyle \left.\vphantom{\frac{s_{Q}(t)}{s_{I}(t)}}\right]$](img772.gif) |
(4.103) |
| |
= |
tan-1![$\displaystyle \left[\vphantom{\tan\left(\frac{\pi t}{2T_{b}}-\frac{\pi}{2}\righ...
...fty}^{+\infty}A_{2k} \textrm{rect}_{[0,2T_{b}]}\left(t-2kT_{b}\right)}}\right.$](img791.gif) tan tan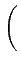 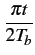 - - 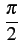 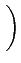 ![$\displaystyle {\frac{{\sum_{k=-\infty}^{+\infty}A_{2k+1} \textrm{rect}_{[0,2T_...
...k=-\infty}^{+\infty}A_{2k} \textrm{rect}_{[0,2T_{b}]}\left(t-2kT_{b}\right)}}}$](img792.gif) ![$\displaystyle \left.\vphantom{\tan\left(\frac{\pi t}{2T_{b}}-\frac{\pi}{2}\righ...
...fty}^{+\infty}A_{2k} \textrm{rect}_{[0,2T_{b}]}\left(t-2kT_{b}\right)}}\right]$](img793.gif) |
(4.104) |
Si maintenant, on observe l'évolution de la phase pendant un intervalle
de temps Tb
d'un bit, la fraction dans l'argument de la fonction
tan-1
vaut 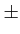 1
et la variation de la phase vaut
1
et la variation de la phase vaut
La phase varie donc linéairement de
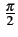 sur la durée
de Tb
secondes. Contrairement aux modulations vues jusqu'ici,
la modulation MSK présente des sauts de phase qui se réalisent en
``douceur''. Par exemple, pour passer de
sur la durée
de Tb
secondes. Contrairement aux modulations vues jusqu'ici,
la modulation MSK présente des sauts de phase qui se réalisent en
``douceur''. Par exemple, pour passer de
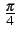 à
à
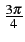 ,
la phase prend Tb
secondes, tandis que l'enveloppe reste constante
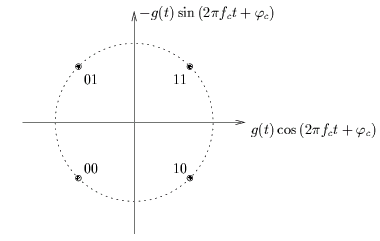
au cours du temps. La figure 4.10 montre en
pointillés les transitions possibles pour la modulation MSK.
,
la phase prend Tb
secondes, tandis que l'enveloppe reste constante
au cours du temps. La figure 4.10 montre en
pointillés les transitions possibles pour la modulation MSK.
Figure 4.10:
Diagramme de constellation pour la modulation MSK.
|
|
On peut également représenter l'évolution de la phase par ce que l'on
appelle le treillis de phase.
Il représente toutes les variations possibles de
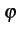 (t)
. La
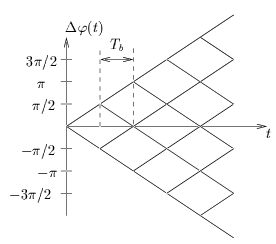
figure 4.11 montre le treillis de phase pour
la modulation MSK. La phase est maintenant une fonction continue du
temps. On peut espérer avoir une bande passante moins importante que
pour la modulation QPSK ou OQPSK.
(t)
. La
figure 4.11 montre le treillis de phase pour
la modulation MSK. La phase est maintenant une fonction continue du
temps. On peut espérer avoir une bande passante moins importante que
pour la modulation QPSK ou OQPSK.
Figure 4.11:
Treillis de phase pour la modulation MSK.
|
|
La figure 4.12 montre un signal modulé MSK pour une séquence
binaire donnée. En observant le signal modulé, on peut également l'interpréter
comme une modulation de fréquence. En effet, en écrivant
s(t) = a(t) cos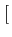 2 2 fct + fct + 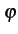 (t) (t)![$\displaystyle \left.\vphantom{2\pi f_{c}t+\varphi(t)}\right]$](img797.gif) |
(4.106) |
et considérant une période Tb
, nous obtenons
| s(t) |
= |
A cos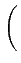 2 2 fct fct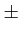 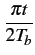 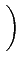 |
(4.107) |
| |
= |
A cos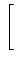 2 2 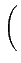 fc fc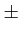 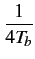 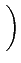 t t![$\displaystyle \left.\vphantom{2\pi\left(f_{c}\pm\frac{1}{4T_{b}}\right)t}\right]$](img803.gif) |
(4.108) |
qui représente bien une modulation de fréquence dont l'excursion est
égale à
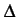 f = 2
f = 2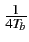 =
= 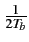 .
.
Figure:
Illustration de la modulation MSK: (a) séquence binaire I(t)
, (b) sI(t)
,
(c) sQ(t)
, (d)
sI(t) cos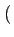 2
2 fct
fct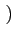 ,
(e)
sQ(t) sin
,
(e)
sQ(t) sin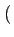 2
2 fct
fct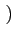 et (f) signal modulé
s(t)
.
et (f) signal modulé
s(t)
.
|
|
L'enveloppe complexe du signal modulé est à nouveau donnée par
es(t) =  Ak g(t - kTb) ejk Ak g(t - kTb) ejk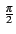 |
(4.109) |
où le signal de mise en forme g(t)
et la variable aléatoire Ak
valent respectivement
| g(t) |
= |
rect[0, 2Tb]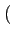 t t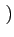 sin sin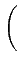 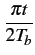 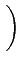 |
(4.110) |
| Ak |
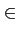 |
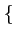 + A, - A + A, - A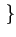 |
(4.111) |
Nous faisons à nouveau l'hypothèse que les deux valeurs possibles
pour Ak
sont équiprobables. La moyenne 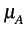 est donc nulle
et la variance est égale à
est donc nulle
et la variance est égale à
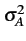 = E
= E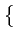 Ak2
Ak2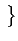 = A2
.
Il vient après calcul de la transformée de FOURIER du signal
de mise en forme
= A2
.
Il vient après calcul de la transformée de FOURIER du signal
de mise en forme
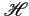 (f )=
(f )= 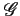
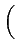 f +
f + 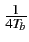
 ,
,
La densité spectrale de puissance d'un signal modulé en MSK s'exprime
donc finalement par
Contrairement à la densité spectrale de puissance de la modulation
OQPSK qui décroît en 1/f2
, la densité spectrale de la modulation
MSK décroît en 1/f4
, ce qui fournit donc un gain en bande passante.
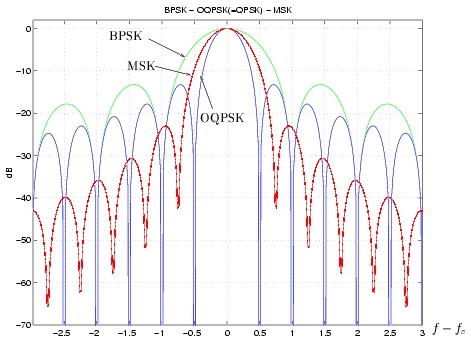
La figure 4.13 permet de comparer les densités spectrales
de puissance des modulation BPSK, OQPSK ( QPSK) et MSK pour
Rb = 1/Tb = 1 [b/s]
. Nous voyons que la décroissance en 1/f4
est accompagnée d'un élargissement du lobe principal par rapport à
la modulation OQPSK.
QPSK) et MSK pour
Rb = 1/Tb = 1 [b/s]
. Nous voyons que la décroissance en 1/f4
est accompagnée d'un élargissement du lobe principal par rapport à
la modulation OQPSK.
Figure 4.13:
Comparaison des densités spectrales de puissance.
|
|
La modulation utilisée pour la transmission GSM est une variante de
la MSK; il s'agit d'une technique appelée Gaussian Minimum Shift Keying
(GMSK) pour laquelle l'onde de mise en forme est une
gaussienne.
Marc Van Droogenbroeck. Tous droits réservés.
2007-10-27

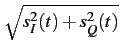
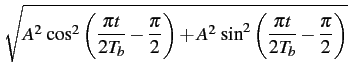
![$\displaystyle {\frac{{\sum_{k=-\infty}^{+\infty}A_{2k+1} \textrm{rect}_{[0,2T_...
...k=-\infty}^{+\infty}A_{2k} \textrm{rect}_{[0,2T_{b}]}\left(t-2kT_{b}\right)}}}$](img792.gif)
![]() (t)
(t)
![]() 2
2![]() fct +
fct + ![]() (t)
(t)![]()
![]() 2
2![]() fct
fct![]()
![]()
![]()
![]() 2
2![]()
![]() fc
fc![]()
![]()
![]() t
t![]()
![]() f = 2
f = 2![]() =
= ![]()
![]() 2
2![]() fct
fct![]()
![]() 2
2![]() fct
fct![]()
![\includegraphics[width=13cm]{images/msk}](img806.gif)
![]() Ak g(t - kTb) ejk
Ak g(t - kTb) ejk![]()
![]() t
t![]() sin
sin![]()
![]()
![]()
![]()
![]() + A, - A
+ A, - A![]()
![]()
![]() = E
= E![]() Ak2
Ak2![]() = A2
= A2
![]() (f )=
(f )= ![]()
![]() f +
f + ![]()
![]()
![]() (f )=
(f )= 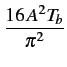
![]()
![$\displaystyle {\frac{{\cos\left[2\pi\left(f+\frac{1}{4T_{b}}\right)T_{b}\right]}}{{1-16\left(f+\frac{1}{4T_{b}}\right)^{2}T_{b}^{2}}}}$](img811.gif)
![]()
![]() (f )=
(f )= 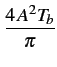
![]()
![]()
![$\displaystyle {\frac{{\cos\left[2\pi\left(f-f_{c}\right)T_{b}\right]}}{{1-16\left(f-f_{c}\right)^{2}T_{b}^{2}}}}$](img816.gif)
![]() +
+ ![]()
![$\displaystyle {\frac{{\cos\left[2\pi\left(f+f_{c}\right)T_{b}\right]}}{{1-16\left(f+f_{c}\right)^{2}T_{b}^{2}}}}$](img819.gif)
![]()
![]()
![]()