Considérons un système de modulation d'impulsions PAM (Pulse Amplitude
Modulation) en bande de base dont le schéma général est représenté
à la figure 5.1. L'information à transmettre
est la séquence binaire {bk}
dont chaque symbole (1 ou 0)
est de durée Tb
. Le modulateur va mettre en forme la séquence
{bk}
, grâce à l'impulsion de mise en forme gE(t)
, et
fournir le signal
s(t) =  Ak gE(t - kTb) Ak gE(t - kTb) |
(5.1) |
où les amplitudes Ak
(représentant l'information binaire transmise
à l'instant t = kTb
) sont liées à la séquence {bk}
par
la relation
Ak = 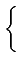 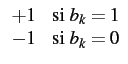 |
(5.2) |
Figure 5.1:
Schéma général de la transmission en bande de base
|
|
Le signal transmis au travers du canal est donc s(t)
.
Celui-ci va être modifié par convolution avec la réponse impulsionnelle
h(t)
du canal de transmission. De plus, un bruit (supposé blanc
et gaussien) vient s'ajouter au signal dans le canal. Le signal reçu,
noté x(t)
, est ensuite filtré par un filtre de réception, de réponse
impulsionnelle gR(t)
. La sortie de ce filtre, notée y(t)
,
est échantillonnée au rythme de l'émetteur, c'est-à-dire toutes les
Tb
secondes et est synchronisé avec celui-ci (les instants d'échantillonnage
sont déterminés par une horloge qui est extraite du signal y(t)
).
Finalement la séquence d'échantillons ainsi obtenue est utilisée pour
reconstruire la séquence originale {bk}
au moyen d'un organe
de décision. L'amplitude de chaque échantillon est comparée à un seuil
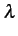 .
.
La sortie du filtre de réception peut s'écrire sous la forme
y(t) =  Ak Ak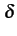 (t - kTb) (t - kTb) 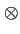 gE(t) gE(t) 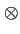 h(t) h(t) 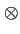 gR(t) + w(t) gR(t) + w(t) 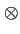 gR(t) gR(t) |
(5.3) |
où le symbole 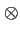 est une convolution. En prenant
les notations suivantes
est une convolution. En prenant
les notations suivantes
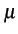 p(t) p(t) |
= |
gE(t) 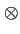 h(t) h(t) 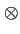 gR(t) gR(t) |
(5.4) |
| n(t) |
= |
w(t)  gR(t) gR(t) |
(5.5) |
où 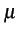 est un facteur d'échelle constant et
est un facteur d'échelle constant et 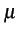 p(t)
est le résultat du passage du signal de mise en forme gE(t)
au travers des deux filtres h(t)
et gR(t)
caractérisant respectivement
le canal et le filtre de réception. Le terme n(t)
est le résidu
du bruit additif w(t)
ajouté par le canal, filtré par le filtre
de réception. Il représente donc toujours un bruit blanc gaussien
car il est passé au travers d'un filtre linéaire. En général, w(t)
est modélisé comme un bruit blanc additif gaussien de moyenne nulle.
On obtient finalement
p(t)
est le résultat du passage du signal de mise en forme gE(t)
au travers des deux filtres h(t)
et gR(t)
caractérisant respectivement
le canal et le filtre de réception. Le terme n(t)
est le résidu
du bruit additif w(t)
ajouté par le canal, filtré par le filtre
de réception. Il représente donc toujours un bruit blanc gaussien
car il est passé au travers d'un filtre linéaire. En général, w(t)
est modélisé comme un bruit blanc additif gaussien de moyenne nulle.
On obtient finalement
y(t) = 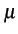  Akp(t - kTb) + n(t) Akp(t - kTb) + n(t) |
(5.6) |
Cette formule montre que le train d'impulsions n'est plus rectangulaire.
Le facteur d'échelle 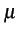 est choisi de telle sorte que le signal
p(t)
soit normalisé, c'est-à-dire
est choisi de telle sorte que le signal
p(t)
soit normalisé, c'est-à-dire
Cette relation justifie l'utilisation de 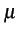 comme facteur d'échelle
pour tenir compte des changements de l'amplitude du signal lors de
son passage à travers le système. De plus, cette relation représente
une contrainte mathématique et n'a aucune signification physique.
Avant de poursuivre, il est important de remarquer que, pour être
rigoureux, il faudrait introduire un délai t0
dans l'argument
de
p(t - kTb)
afin de représenter l'effet du délai de la transmission
au travers du système. Cependant, pour simplifier l'exposé, nous choisissons
de prendre ce délai égal à zéro, et cela sans perdre en généralité.
comme facteur d'échelle
pour tenir compte des changements de l'amplitude du signal lors de
son passage à travers le système. De plus, cette relation représente
une contrainte mathématique et n'a aucune signification physique.
Avant de poursuivre, il est important de remarquer que, pour être
rigoureux, il faudrait introduire un délai t0
dans l'argument
de
p(t - kTb)
afin de représenter l'effet du délai de la transmission
au travers du système. Cependant, pour simplifier l'exposé, nous choisissons
de prendre ce délai égal à zéro, et cela sans perdre en généralité.
Vu qu'une convolution dans le domaine temporel équivaut à un produit
dans le domaine fréquentiel, nous déduisons de la relation 5.4
que
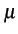 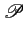 (f )= (f )= 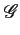 E(f ) E(f )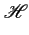 (f ) (f )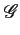 R(f ) R(f ) |
(5.8) |
Le signal y(t)
à la sortie du filtre de réception est échantillonné
aux instants
ti = iTb
(il est intéressant de rappeler que l'échantillonnage
se fait à la fin de la période, ceci résultant de la théorie de du
filtre adapté), ce qui fournit les échantillons
| y(ti) |
= |
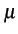  Akp((i - k)Tb) + n(ti) Akp((i - k)Tb) + n(ti) |
(5.9) |
| |
= |
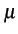 Ai + Ai + 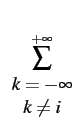 Akp((i - k)Tb) + n(ti) Akp((i - k)Tb) + n(ti) |
(5.10) |
Le premier terme 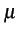 Ai
représente la contribution du i
-ème
bit transmis et donc le symbole d'intérêt. Le second terme représente
l'effet résiduel de tous les autres bits transmis sur le i
-ème
bit, qu'ils aient été transmis avant ou après le i
-ème bit. Cet
effet résiduel est appelé interférence inter-symboles.
L'importance de cet effet dépend de l'étalement de p(t)
. On peut
déjà remarquer que pour minimiser le terme d'interférence inter-symboles,
il faudra choisir une forme adéquate pour la fonction p(t)
de manière
à éliminer ce second terme. Le dernier terme de n(ti)
est le
bruit n(t)
échantillonné à l'instant ti
.
Ai
représente la contribution du i
-ème
bit transmis et donc le symbole d'intérêt. Le second terme représente
l'effet résiduel de tous les autres bits transmis sur le i
-ème
bit, qu'ils aient été transmis avant ou après le i
-ème bit. Cet
effet résiduel est appelé interférence inter-symboles.
L'importance de cet effet dépend de l'étalement de p(t)
. On peut
déjà remarquer que pour minimiser le terme d'interférence inter-symboles,
il faudra choisir une forme adéquate pour la fonction p(t)
de manière
à éliminer ce second terme. Le dernier terme de n(ti)
est le
bruit n(t)
échantillonné à l'instant ti
.
En l'absence d'interférence inter-symboles et de bruit, l'équation 5.10
se réduit à
y(ti) = 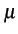 Ai Ai |
(5.11) |
ce qui montre bien que, sous ces conditions idéales, le i
-ème bit
transmis est décodé correctement. La présence inévitable d'interférence
inter-symboles et de bruit dans le système introduit des erreurs au
niveau de l'organe de décision. Dès lors, lors la conception du filtre
de mise en forme et du filtre de réception, l'objectif est de minimiser
les effets de l'interférence inter-symboles et du bruit, aboutissant
ainsi à un taux d'erreurs aussi faible que possible.
Il existe deux types de transmission:
- la transmission où le bruit est prépondérant, c'est le cas des communications
satellite par exemple, pour lequel on privilégie le bon fonctionnement
du filtre adapté,
- la transmission où le rapport signal sur bruit est important, comme
pour le cas du réseau téléphonique par exemple, et dès lors le fonctionnement
du système est essentiellement limité par l'interférence inter-symboles,
et non par le bruit.
Dans l'étude qui suit, nous nous placerons dans le second cas et nous
négligeons ainsi le terme n(t)
et nous nous focalisons sur la question
de la réduction, voire de l'élimination de l'interférence inter-symboles.
Marc Van Droogenbroeck. Tous droits réservés.
2007-10-27
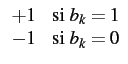
![]()
![]() Ak
Ak![]() (t - kTb)
(t - kTb) ![]() gE(t)
gE(t) ![]() h(t)
h(t) ![]() gR(t) + w(t)
gR(t) + w(t) ![]() gR(t)
gR(t)![]()
![]()
![]() p(t)
p(t)
![]()
![]()
![]() Ai
Ai
![]() Ai
Ai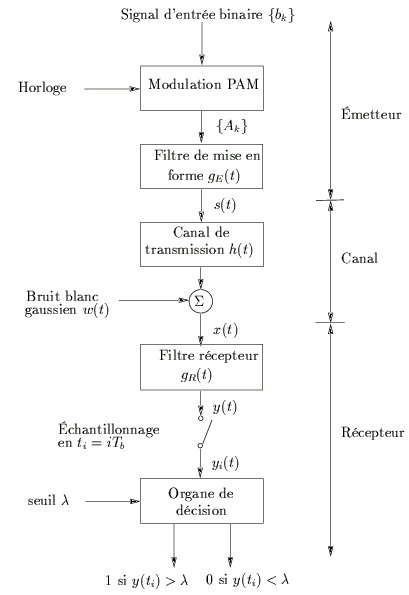
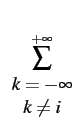 Akp((i - k)Tb) + n(ti)
Akp((i - k)Tb) + n(ti)