6.2.1 Principes de base de l'étalement direct

Avant d'aborder les développements mathématiques, prenons un exemple simple permettant d'illustrer le principe de l'étalement. Dans un système à étalement de spectre, on considère deux types de signaux:

1. le signal contenant les données à transmettre, de période T_b ,
2. le signal permettant d'effectuer l'étalement, de période T_c (on parle de ``chip''), nettement plus petite que T_b .

Par la suite, nous prendrons

T_b = NT_c (6.1)

Considérons la figure 6.1. Le premier signal représente le signal de données binaires à transmettre (ici, deux bits) ainsi que l'occupation spectrale associée (idéalisée). Le deuxième signal représente un exemple de séquence d'étalement. On constate que son occupation spectrale est dilatée par N .

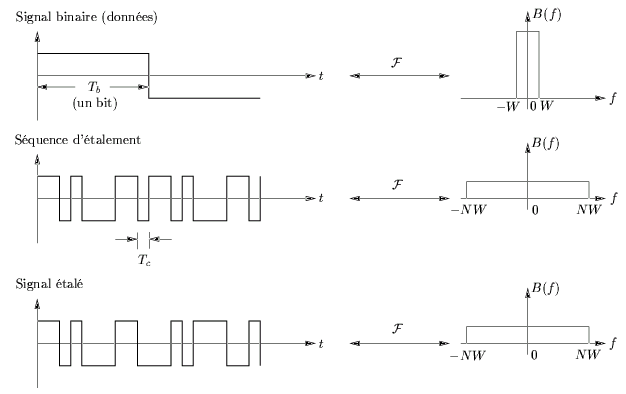
Dans un système à étalement direct, le taux de transmission de symboles (1/T_b) d'un signal bipolaire binaire est augmenté en multipliant cette onde par un code bipolaire binaire pseudo-aléatoire périodique dont la durée T_c est nettement plus courte que celle de départ; on obtient alors un signal tel que celui représenté à la troisième ligne de la figure 6.1. Son spectre est approximativement aussi large que celui de la séquence d'étalement.

Figure 6.1: Exemple d'étalement d'un signal de données binaires.

 

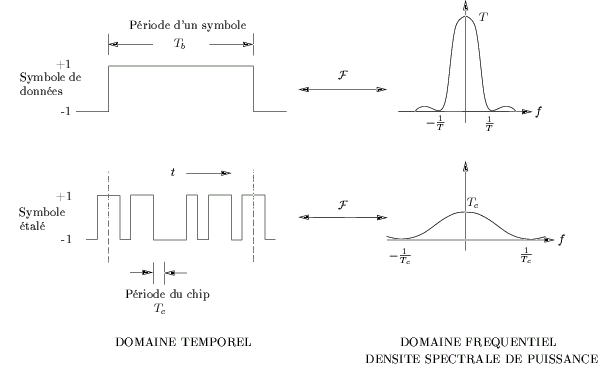
La figure 6.2 donne une représentation plus exacte des densités spectrales de puissance du signal de données et de la séquence d'étalement et illustre bien le théorème de conservation de l'énergie (conservation de l'aire sous la courbe).

Figure 6.2: Effet de la multiplication par une séquence sur le spectre.

 

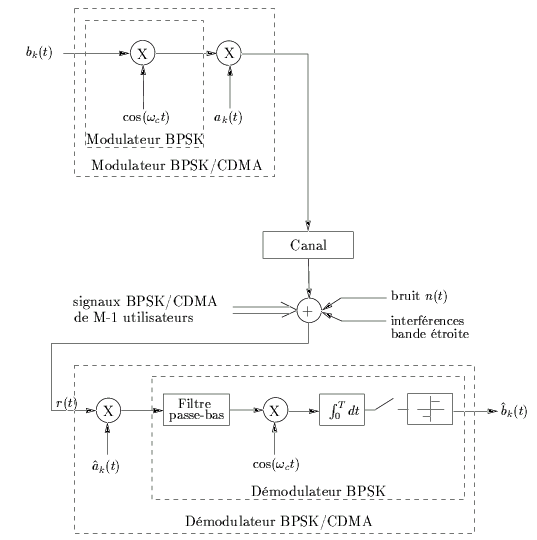
Dans un système à étalement direct, deux étages de modulation sont utilisés. Dans le premier étage, le signal numérique en bande de base est mélangé à une séquence numérique pseudo-aléatoire à large bande. Le résultat de cette modulation fournit un signal à large bande qui sera modulé, dans le second étage de modulation, par une technique de modulation de phase numérique (BPSK par exemple). La figure montre un tel schéma d'un modulateur - démodulateur à étalement direct de spectre.

Figure 6.3: Bloc diagramme d'un système à étalement direct de spectre.

 

Les séquences d'étalement ont pour but de faire apparaître, pour l'utilisateur courant, les autres utilisateurs comme du bruit. Ces séquences doivent dès lors avoir les caractéristiques les plus proches possible de celles d'un bruit blanc. Néanmoins, pour que le récepteur puisse retrouver le signal utile, il doit aussi être capable de régénérer la séquence ayant servi à l'étalement. Il ne peut donc s'agir d'une véritable séquence aléatoire mais bien d'une séquence déterministe ayant des propriétés aussi proches que possibles de celles d'une séquence aléatoire; on parle donc de séquences pseudo-aléatoires. De plus, pour des raisons pratiques de réalisation, les séquences sont périodiques.

Pour construire des générateurs de séquences pseudo-aléatoires, on peut partir de l'étude des propriétés des séquences aléatoires et imposer algébriquement des propriétés similaires aux générateurs. C'est la démarche que nous suivrons ici. Une remarque s'impose néanmoins: il est possible de construire plusieurs types de générateurs de séquences aléatoires. L'étude menée dans ce document ne se veut donc pas exhaustive. Le lecteur est invité à consulter des ouvrages spécialisés pour une typologie des générateurs de séquences pseudo-aléatoires.