Sous-sections
Une séquence pseudo-aléatoire est une séquence binaire périodique
dont l'onde ressemble, mis à part le caractère périodique, à une séquence
binaire totalement aléatoire proche d'un bruit. Ce type de séquences
est par exemple généré à l'aide d'un registre à décalage à contre-réaction,
dont le schéma général est montré à la figure 6.4.
Figure 6.4:
Registre à décalage à contre-réaction.
|
|
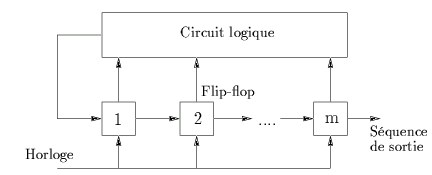
Ce registre est constitué de m
flip-flops (éléments mémoire) et
d'un circuit logique qui sont interconnectés pour former un circuit
à contre-réaction. Les flip-flops sont régulés par une seule horloge.
À chaque coup d'horloge, le contenu de chaque flip-flop est décalé
d'une place vers la droite. De même, à chaque coup d'horloge, le circuit
logique calcule une fonction booléenne du contenu des m
flip-flops
et le résultat est réinjecté à l'entrée du registre. La séquence pseudo-aléatoire
est ainsi déterminée par le nombre m
de flip-flops, l'état initial
du registre et la fonction booléenne implémentée.
Avec un nombre m
de flip-flops, le registre peut avoir 2m
états possibles . Ainsi, la séquence pseudo-aléatoire, issue de la
sortie du dernier flip-flop, peut avoir au maximum une période de
2m
. Lorsque le circuit logique est constitué uniquement d'additionneurs
modulo-2, le registre est dit linéaire et l'état 0 (zéro dans
chaque flip-flop) n'est pas permis sinon la séquence pseudo-aléatoire
reste indéfiniment nulle. Dès lors, une séquence pseudo-aléatoire
générée par un registre à décalage linéaire ne peut avoir qu'une période
maximale de 2m - 1
. On parle alors de séquence de longueur
maximale.
Tout l'art de la conception du circuit consiste à synthétiser une
fonction booléenne génératrice d'une séquence se rapprochant au mieux
d'une séquence aléatoire.
Exemple. Considérons le registre à décalage linéaire
de la figure 6.5.
Figure 6.5:
Exemple de registre à décalage linéaire.
|
|
L'état initial du registre est supposé être 100 (lorsqu'on
lit le contenu des flip-flops de la gauche vers la droite). Les états
successifs du registre sont
100, 110, 111
,
011, 101, 010
,
001, 100, ...
La séquence de sortie est alors égale à
00111010...
,
qui se répète avec une période 23 - 1 = 7
. Il est à noter que l'état
initial est arbitraire mais non nul.
Les séquences de longueur maximale ont des propriétés proches de celles
des séquences binaires purement aléatoires6.1.
Considérons des symboles 0 et 1 respectivement représentés par les
niveaux -1
et +1
. Voici quelques propriétés des séquences pseudo-aléatoires
- durant chaque période d'une séquence pseudo-aléatoire, il y a toujours
un symbole 1
de plus que de 0
-le choix d'avoir plus de 1
que de 0
plutôt que l'inverse est arbitraire. Dès lors,
- la fonction d'autocorrélation d'une séquence de longueur maximale
est périodique.
Détaillons quelque peu cette dernière propriété. La période d'une
séquence de longueur maximale est définie par
Appelons c(t)
l'onde résultante de la séquence de longueur maximale,
comme illustré à la figure 6.6(a) pour
N = 7
. La période de l'onde c(t)
est égale à
où Tc
, appelée période chip, est la durée d'un
bit de la séquence de longueur maximale. Par définition, la fonction
d'autocorrélation d'un signal périodique c(t)
de période Tb
est
où 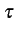 appartient à l'intervalle
[- Tb/2, + Tb/2]
. En appliquant
cette formule à la séquence de longueur maximale c(t)
, on obtient
appartient à l'intervalle
[- Tb/2, + Tb/2]
. En appliquant
cette formule à la séquence de longueur maximale c(t)
, on obtient
Ce résultat est montré à la figure 6.6(b)
pour m = 3
et N = 7
.
Figure 6.6:
Propriétés d'une séquence de longueur maximale.
|
|
Étant donné qu'une périodicité dans le domaine temporel correspond
à un échantillonnage uniforme dans le domaine fréquentiel, et la forme
de la fonction d'autocorrélation de c(t)
, on peut déterminer la
densité spectrale de puissance de c(t)
qui est représentée à la figure 6.6(c)
pour m = 3
et N = 7
. Au vu de ces résultats, il est maintenant possible
de comparer une séquence de longueur maximale et une séquence réellement
aléatoire:
- sur une période de la séquence de longueur maximale, la fonction d'autocorrélation
de c(t)
est similaire à celle de la séquence aléatoire. En effet,
la fonction d'autocorrélation d'une séquence aléatoire vaut
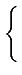  |
(6.8) |
Il apparaît donc que les densités spectrales des deux séquences ont
une même enveloppe, à savoir
sinc2(fT)
.
- la différence fondamentale réside dans le fait que le spectre de la
séquence aléatoire est continu tandis que celui de la séquence de
longueur maximale est composé de raies espacées de 1/NTc
.
Lorsque l'on augmente la valeur de N
, c'est-à-dire le longueur
de la séquence de longueur maximale, la séquence pseudo-aléatoire
se rapproche plus d'une séquence aléatoire pure. Cependant, le prix
à payer avec une grande valeur de N
, est une augmentation de la
bande passante nécessaire. Un compromis doit dès lors être établi.
La question qui se pose à présent est: comment choisir la fonction
logique du registre à décalage pour obtenir une période désirée N
?
La littérature fournit des tables avec les connections à réaliser
entre les éléments du circuit pour différentes valeurs de m
. Une
telle table est montrée à la figure 6.7.
Figure 6.7:
Table permettant de construire le registre à décalage adéquat [15, page 584].
|
|
Plus m
augmente, plus il y a de possibilités de circuits.
Exemple. Considérons une séquence de longueur maximale
nécessitant l'utilisation d'un registre de longueur m = 5
. Pour cette
valeur de m
, nous choisissons dans la table une boucle à rétroaction
du type [5, 2]
. La configuration correspondante est montrée à
la figure 6.8(a). En supposant un état
initial 10000, la figure 6.2 montre
l'évolution du registre pour une période de la séquence de longueur
maximale. On remarque qu'en fin de période, le registre est revenu
à son état initial. On aurait également pu choisir la configuration
[5, 4, 2, 1]
comme le montre la figure 6.8(b)
et on aurait une autre séquence pseudo-aléatoire de même longueur.
Figure 6.8:
Deux schémas possibles pour m = 5
[15, page 584].
|
|
Tableau 6.2:
Évolution du registre de la figure 6.8(a)
au cours d'une période de la séquence [15, page 585].
| |
Registres |
|
| Bit de rétroaction |
1 |
0 |
0 |
0 |
0 |
Bit de sortie |
| 0 |
0 |
1 |
0 |
0 |
0 |
0 |
| 1 |
1 |
0 |
1 |
0 |
0 |
0 |
| 0 |
0 |
1 |
0 |
1 |
0 |
0 |
| 1 |
1 |
0 |
1 |
0 |
1 |
0 |
| 1 |
1 |
1 |
0 |
1 |
0 |
1 |
| 1 |
1 |
1 |
1 |
0 |
1 |
0 |
| 0 |
0 |
1 |
1 |
1 |
0 |
1 |
| 1 |
1 |
0 |
1 |
1 |
1 |
0 |
| 1 |
1 |
1 |
0 |
1 |
1 |
1 |
| 0 |
0 |
1 |
1 |
0 |
1 |
1 |
| 0 |
0 |
0 |
1 |
1 |
0 |
1 |
| 0 |
0 |
0 |
0 |
1 |
1 |
0 |
| 1 |
1 |
0 |
0 |
0 |
1 |
1 |
| 1 |
1 |
1 |
0 |
0 |
0 |
1 |
| 1 |
1 |
1 |
1 |
0 |
0 |
0 |
| 1 |
1 |
1 |
1 |
1 |
0 |
0 |
| 1 |
1 |
1 |
1 |
1 |
1 |
0 |
| 0 |
0 |
1 |
1 |
1 |
1 |
1 |
| 0 |
0 |
0 |
1 |
1 |
1 |
1 |
| 1 |
1 |
0 |
0 |
1 |
1 |
1 |
| 1 |
1 |
1 |
0 |
0 |
1 |
1 |
| 0 |
0 |
1 |
1 |
0 |
0 |
1 |
| 1 |
1 |
0 |
1 |
1 |
0 |
0 |
| 0 |
0 |
1 |
0 |
1 |
1 |
0 |
| 0 |
0 |
0 |
1 |
0 |
1 |
1 |
| 1 |
1 |
0 |
0 |
1 |
0 |
1 |
| 0 |
0 |
1 |
0 |
0 |
1 |
0 |
| 0 |
0 |
0 |
1 |
0 |
0 |
1 |
| 0 |
0 |
0 |
0 |
1 |
0 |
0 |
| 0 |
0 |
0 |
0 |
0 |
1 |
0 |
| 1 |
1 |
0 |
0 |
0 |
0 |
1 |
|
Notes
- ... aléatoires6.1
- L'utilisation d'une séquence réellement aléatoire ne permettrait pas
de restituer le signal utile au récepteur précisément en raison de
l'aspect aléatoire!
Marc Van Droogenbroeck. Tous droits réservés.
2007-10-27
![]() c(t)
c(t)![]() =
= ![]()
![]()
![]()
![]()
![]() =
= ![]()
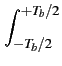 c(t)c(t +
c(t)c(t + ![]() )d
)d![]()
![]()
![]()
![]()
![]()
![]() =
= ![]()
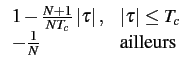
![]() (f )=
(f )= ![]()
![]() (f )+
(f )+ 
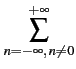
![]()
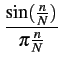
![]()
![]()
![]() f -
f - ![]()
![]()