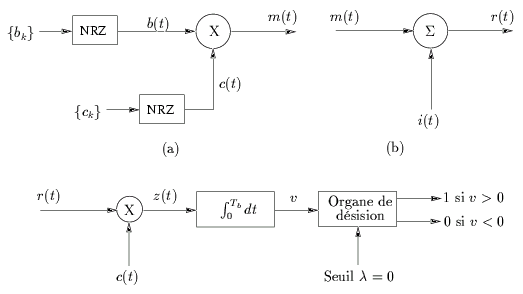
Soit la séquence binaire {bk}
représentant l'information à
transmettre. Cette séquence conduit à définir une onde continue b(t)
par un codage de type NRZ bipolaire 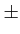 1
. De même, on constitue
un signal temporel c(t)
à partir des éléments {ck}
d'une
séquence pseudo-aléatoire.
1
. De même, on constitue
un signal temporel c(t)
à partir des éléments {ck}
d'une
séquence pseudo-aléatoire.
L'étalement du spectre de b(t)
se réalise au moyen d'une modulation
qui n'est autre que la multiplication de c(t)
et b(t)
, comme
le montre la figure 6.9(a).
Figure 6.9:
Modèle d'une transmission à spectre étalé en bande de base.
|
|
Or, une multiplication dans le domaine temporel revient à faire une
convolution dans le domaine fréquentiel. Dès lors, si le signal b(t)
est à bande étroite et que c(t)
est à large bande, le spectre du
signal résultant
sera pratiquement aussi large que celui de c(t)
. En effet,
 (f ) (f ) |
= |
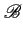 (f ) (f ) 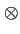 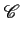 (f ) (f ) |
(6.10) |
| |
= |
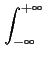 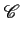 ( (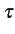 ) )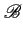 (f - (f - 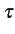 ) d ) d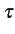 |
(6.11) |
Or, on effectue le produit des deux courbes et on intègre
sur toutes les valeurs différentes de zéro. On obtient dès lors un
signal large bande. De plus, la figure 6.10
montre très clairement que la période du signal étalé est de Tc
et donc la bande de base du signal étalé vaut
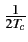 ,
ce qui représente un signal large bande.
,
ce qui représente un signal large bande.
On dit que la séquence c(t)
joue le rôle de code d'étalement.
La formation du signal m(t)
est montrée à la figure 6.10.
Figure 6.10:
Formation du signal m(t)
par étalement du spectre de b(t)
.
|
|
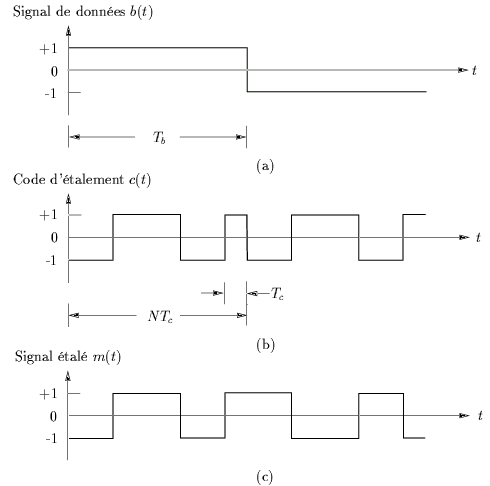
Pour une transmission en bande de base, on transmet le signal
m(t)
sur le canal .
Le récepteur reçoit le signal étalé m(t)
bruité par des interférences
caractérisées par le signal i(t)
(cf. figure 6.9(b))
| r(t) |
= |
m(t) + i(t) |
(6.12) |
| |
= |
c(t)b(t) + i(t) |
(6.13) |
Le signal d'interférence se compose de signaux émis par d'autres utilisateurs
dans la même bande de fréquences ainsi que du bruit.
Pour recouvrer le signal original et la séquence binaire sous-jacente,
le signal reçu r(t)
est appliqué à l'entrée d'un démodulateur qui
consiste en un mélangeur suivi d'un intégrateur et d'un organe de
décision, comme l'illustre la figure 6.9(c).
Au niveau du mélangeur, le signal reçu r(t)
est multiplié par une
réplique exacte de la séquence pseudo-aléatoire utilisée au récepteur.
Nous faisons l'hypothèse que le récepteur travaille en synchronisation
parfaite avec l'émetteur. La sortie du mélangeur est alors donnée
par
| z(t) |
= |
c(t)r(t) |
(6.14) |
| |
= |
c2(t)b(t) + c(t)i(t) |
(6.15) |
Cette dernière équation montre que le signal b(t)
est multiplié
deux fois par la séquence pseudo-aléatoire c(t)
, tandis que le
signal i(t)
n'est multiplié qu'une seule fois. Vu que c(t)
vaut
+1
ou -1
, le signal c2(t)
est égal à 1 pour tout instant
t
. Donc, le signal z(t)
se réduit à
| z(t) = b(t) + c(t)i(t) |
(6.16) |
Nous voyons donc que le signal b(t)
, qui contient l'information
utile, se retrouve à la sortie du mélangeur. Si le terme additif c(t)i(t)
semble gênant, il faut bien voir que la multiplication de i(t)
par le code d'étalement c(t)
a pour effet d'étaler le spectre de
i(t)
. Dès lors, le signal c(t)i(t)
est à large bande tandis
que le signal b(t)
est à bande étroite. Ce signal large bande contient
notamment les signaux étalés des autres utilisateurs, ceux-ci étant
considérés comme du bruit.
En appliquant le signal z(t)
à l'entrée d'un filtre passe-bas,
en l'occurrence l'intégrateur, la majeure partie de l'énergie de c(t)i(t)
est filtrée. L'effet de l'interférence i(t)
est donc fortement
réduit à la sortie du récepteur. En réalité, à partir du signal z(t)
,
tout se passe comme pour la démodulation d'un signal numérique par
le filtre adapté suivi de l'organe de décision. Le signal b(t)
est le signal numérique à démoduler et c(t)i(t)
peut être vu comme
l'approximation d'un bruit blanc additif gaussien. Plus la séquence
pseudo-aléatoire est longue, plus cette approximation est vérifiée.
Cependant, le prix à payer pour cette augmentation de la protection
contre les interférences est une augmentation de la bande passante
requise, de la complexité du système, ainsi que des délais.
En résumé, l'utilisation d'un code d'étalement dans l'émetteur produit
un signal large bande transmis sur le canal. Celui-ci apparaît comme
du bruit pour un récepteur qui n'a pas connaissance du code d'étalement
initial.
Marc Van Droogenbroeck. Tous droits réservés.
2007-10-27
![]() (f )
(f )![]() (f )
(f ) ![]()
![]() (f )
(f )![]()
![]() (
(![]() )
)![]() (f -
(f - ![]() ) d
) d![]()
![]()