6.2.4 Étalement direct par modulation BPSK

Nous allons à présent voir comment on peut intégrer la notion d'étalement direct de spectre dans un système de modulation. Le type de modulation choisie est une modulation de phase binaire cohérente (BPSK).

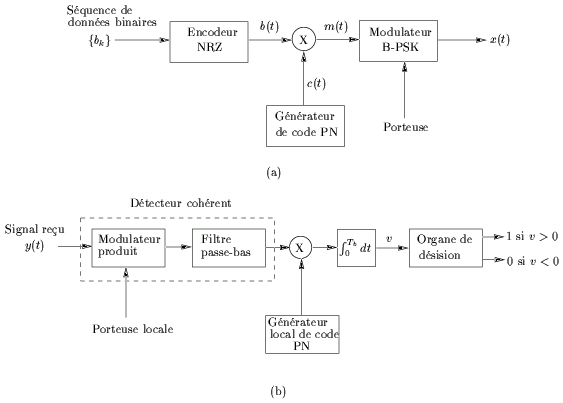
La figure 6.11(a) montre le schéma d'un tel modulateur. Le modulateur transforme tout d'abord la séquence {b_k} en signal NRZ bipolaire pour obtenir le signal b(t) . Il y a ensuite deux étages de modulation: le premier étage multiplie le signal b(t) par la séquence pseudo-aléatoire c(t) tandis que le deuxième étage est un modulateur BPSK. Le message transmis x(t) est alors un signal modulé en DS/BPSK (Direct-Sequence spread Binary Phase Shift-Keying). La phase 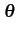$\theta$(t) du signal modulé x(t) vaut 0 ou $\pi$ selon que les signaux b(t) et c(t) sont de même polarité ou non à l'instant t . Un saut de phase est ainsi observé tous les T_c .

Figure 6.11: Schéma-bloc de la modulation DS/BPSK.

 

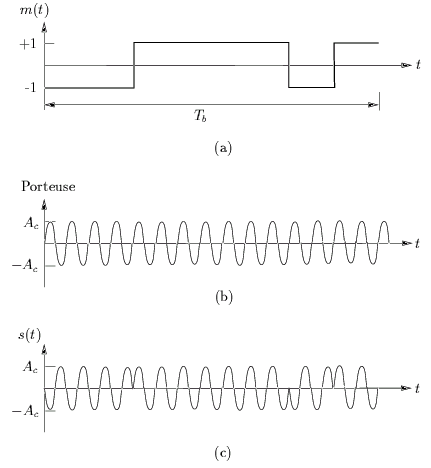
La figure 6.12 illustre la formation du signal modulé BPSK. La figure 6.12.(c) représente donc le signal qui sera envoyé sur le canal pour la transmission d'un bit.

Figure 6.12: Modulation BPSK du signal.

 

Le récepteur, illustré à la figure 6.11(b) est composé de deux étages. Au niveau du premier étage, le signal reçu y(t) est appliqué à l'entrée d'un démodulateur cohérent BPSK, constitué d'un mélangeur alimenté par une porteuse générée localement, suivi d'un filtre passe-bas dont la bande passante est limitée à celle de m(t) . Le deuxième étage de démodulation effectue le ``désétalement'' du spectre en multipliant la sortie du filtre passe-bas par la copie exacte de la séquence pseudo-aléatoire utilisée à l'émetteur. Le reste de la démodulation est identique à celle utilisée pour la transmission en bande de base (filtre adapté et organe de décision).

6.2.4.1 Analyse

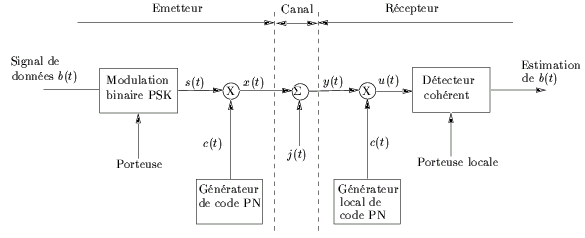
La figure 6.11 représente un modulateur où l'étalement de spectre se fait avant la modulation de phase numérique. Pour une analyse plus détaillée, il est intéressant d'intervertir -conceptuellement- ces deux étapes de modulation comme le montre le schéma de la figure 6.13. Cette permutation est licite car les opérations d'étalement de spectre et de modulation BPSK sont linéaires. Il en va de même pour les opérations de démodulation. Le fait de permuter les deux opérations permet de modifier la réponse impulsionnelle du filtre adapté qui, pour rappel, est donnée par

h(t) = g(T_b - t) (6.17)

Combinant les deux opérations, g(t) devient cos(2$\pi$f_ct) . La réponse impulsionnelle du filtre adapté sera donc un cosinus retourné.

Figure 6.13: Permutation entre étalement et modulation de phase

 

Les interférences sont modélisées par le signal j(t) qui est de type passe-bande. La sortie du canal y(t) s'exprime donc par

y(t) = x(t) + j(t) (6.18)

= c(t)s(t) + j(t) (6.19)

où s(t) est le résultat de la modulation BPSK du signal b(t) .

Au récepteur, le signal reçu y(t) est tout d'abord multiplié par la séquence pseudo-aléatoire c(t) , ce qui donne le signal

u(t) = c(t)y(t) (6.20)

= c²(t)s(t) + c(t)j(t) (6.21)

= s(t) + c(t)j(t) (6.22)

Cette dernière équation montre que le signal à l'entrée du démodulateur cohérent BPSK est un signal modulé en BPSK augmenté de l'interférence c(t)j(t) . La démodulation peut alors se faire, comme pour le cas de la transmission en bande de base, en utilisant un filtre adapté suivi d'un organe de décision, le terme d'interférence étant considéré comme un bruit blanc additif gaussien.