C'est une règle générale que l'utilisation d'une bande de fréquence
plus large accroît la résistance au bruit. Dès lors qu'un utilisateur
est seul à utiliser un large canal, il bénéficiera d'un qualité de
transmission idéale. Une telle situation est néanmoins rare car elle
entraîne un gaspillage de ressources qui ne se justifie pas. En pratique
donc, un utilisateur partage le canal avec d'autres utilisateurs.
Le nombre d'utilisateurs simultanés dans une même bande de fréquence
est appelée capacité. La proposition suivante établit un résultat
important pour le calcul de la capacité des techniques d'étalement
de spectre.
.
De la même manière, la puissance de bruit à l'entrée de la station
de base vaut
Dès lors, le rapport de la puissance de porteuse d'un mobile à l'entrée
de la station de base vaut
Soit M
le nombre de mobiles traités par la cellule. En supposant
que tous les émetteurs travaillent à même niveau de puissance et en
négligeant le bruit thermique, les autres mobiles produisent une puissance
d'interférence
ce qui conduit à
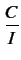 = = 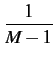 |
(6.34) |
En combinant les deux expressions de
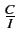 , on en déduit
, on en déduit
On voit donc que la capacité de la cellule est bien proportionnelle
au gain d'étalement
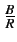 . M
est donc approximativement
égal à la marge d'interférence. Dans l'exemple du paragraphe précédent,
on observe un nombre d'utilisateurs égal à
M = 101, 51
. M
est donc approximativement
égal à la marge d'interférence. Dans l'exemple du paragraphe précédent,
on observe un nombre d'utilisateurs égal à
M = 101, 51 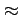 32
.
On voit dès lors que, plus on veut mettre des utilisateurs sur la
même bande de fréquences pour une même probabilité d'erreur, plus
le gain d'étalement doit être important et donc plus B
doit être
élevé par rapport à R
, et donc, plus Tc
doit être petit par
rapport à Tb
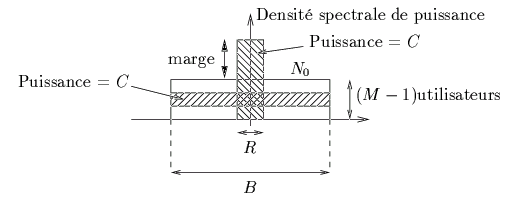
. Une interprétation intéressante est montrée à
la figure 6.14; la puissance de l'utilisateur
ramenée dans une bande large de R [Hz]
dépasse largement la puissance
d'interférence des autres utilisateurs.
32
.
On voit dès lors que, plus on veut mettre des utilisateurs sur la
même bande de fréquences pour une même probabilité d'erreur, plus
le gain d'étalement doit être important et donc plus B
doit être
élevé par rapport à R
, et donc, plus Tc
doit être petit par
rapport à Tb
. Une interprétation intéressante est montrée à
la figure 6.14; la puissance de l'utilisateur
ramenée dans une bande large de R [Hz]
dépasse largement la puissance
d'interférence des autres utilisateurs.
Figure 6.14:
Interprétation de l'étalement de spectre.
|
|
Mais on peut encore faire d'autres gains permettant d'augmenter le
nombre d'utilisateurs sur une cellule. En effet, lors d'une conversation,
les temps morts occupent une partie non négligeable du temps total.
Des études ont montré que le temps de conversation est de l'ordre
de 35%
du temps total de la communication. Comme, en pratique,
on ne coupe pas instantanément le message dès détection d'un silence,
on considère plutôt un facteur d'occupation
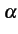 de 50%
, ce qui statistiquement mène à un nombre d'utilisateurs
simultanés
de 50%
, ce qui statistiquement mène à un nombre d'utilisateurs
simultanés
À ce dernier calcul s'ajoute une autre considération relative à la
directivité des antennes. Pour une même cellule, on place généralement
plusieurs antennes (typiquement trois), chacune ayant une directivité
telle qu'elle est responsable de la couverture d'une portion de la
cellule, ce qui divise la zone de rayonnement de la cellule en plusieurs
secteurs. Ceci permettrait d'augmenter le nombre d'utilisateurs dans
une même cellule par un facteur trois, mais pour éviter un trou de
couverture, on assure un certain recouvrement (par exemple 15%
).
Le tout amène un gain G
supplémentaire, égal à
3 x 0, 85
,
conduisant à une valeur de M
de
Enfin, considérant trois cellules trisectorielles, la technique de
CDM implique l'utilisation des mêmes fréquences pour toutes les cellules
(on utilise toute la bande passante), ce qui implique un certain recouvrement
qui se traduit par un facteur de réutilisation de fréquence Fe
inférieur à l'unité.
Fe =  |
(6.38) |
Ce qui donne l'estimation suivante pour le nombre d'utilisateurs
par cellule
Pour le GSM,
Fe 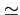 1
.
1
.
Marc Van Droogenbroeck. Tous droits réservés.
2007-10-27
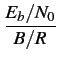
![]() =
= 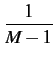
![]()
![]()
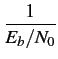 +1
+1 ![]()
![]()
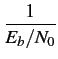
![]()
![]() 32
32
![]()
![]()
![]()
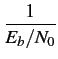
![]()
![]()
![]()
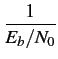
![]() G
G
![]()
![]()
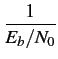
![]() GFe
GFe![]() 1
1