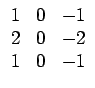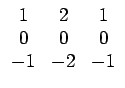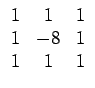Sous-sections
6.1.5 Expressions pratiques d'opérateurs de gradient et masques de convolution
À partir des différents opérateurs discrets introduits plus haut,
nous allons voir comment définir différentes formes de base de filtre
ainsi que les masques de convolution que l'on pourra appliquer directement
aux images échantillonnées.
Le passage le plus simple des expressions analytiques valables pour
des images continues à des images échantillonnées s'effectue en considérant
un pas d'échantillonnage h identique en x et en y. Par convention,
h est choisi égal à 1; dès lors,
f (x + h, y) représente alors
le pixel situé juste à droite (ou à gauche selon l'orientation de
l'axe x) du pixel f (x, y).
L'approximation la plus sommaire de la dérivée première dans la direction
x consiste à prendre la différence entre deux pixels voisins en
utilisant le masque de convolution
suivant6.1
ce qui correspond en fait à l'approximation non-centrée suivante
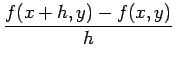 |
(6.33) |
Ce masque présente un inconvénient majeur: le résultat est décalé
d'un demi pixel par rapport aux points utilisés pour le calcul. On
lui préfère généralement le masque étendu suivant
qui correspond à l'approximation centrée décrite en détail précédemment.
Ce petit masque s'applique directement sur la grille des pixels de
l'image que l'on désire traiter, en plaçant le 0 sur le pixel en cours
de traitement. Une approximation de la dérivée première dans la direction
y est donnée par
Dans la foulée, on peut imaginer l'utilisation du masque suivant
pour procéder à une dérivation directionnelle dans la direction diagonale
1350. La figure 6.5 montre le résultat
de l'application de divers opérateurs de dérivée. L'image originale
est définie sur 8 bits de luminance; les images gradients ont été
décalées de 128.
Figure 6.5:
Illustrations de l'application de masques de dérivée première: (a)
image originale, (b) application d'un masque horizontal, (c) application
d'un masque vertical et (d) application d'un masque à 1350.
|
|
L'utilisation des masques de convolution pose quelques problèmes pratiques:
- Effets de bord. L'application
d'un masque est délicate près d'un bord puisqu'il faudrait inclure
des valeurs qui ne se situent hors image. Ce problème récurrent pour
l'application d'opérateurs locaux est résolu de différentes manières,
selon le type de l'opérateur:
- (i) placement d'une valeur hors image par défaut; cette
valeur dépendra de l'opérateur appliqué,
- (ii) miroirisation, qui consiste à miroiriser les valeurs de
l'intérieur vers l'extérieur de l'image,
- (iii) périodisation de l'image -on retrouve alors les pixels
de la gauche contre les pixels du bord droit-, qui se justifie par
la périodisation spatiale subséquente à l'échantillonnage du spectre,
- (iv) recopiage des valeurs du bord de l'image. Cette opération
consiste à recopier les valeurs des lignes et colonnes qui forment
le bord intérieur de l'image.
- Modifications de la dynamique de
valeurs. Le résultat de l'opérateur n'est pas nécessairement compris
dans la dynamique de départ. En effet, considérons une image définie
sur l'intervalle [0, 255]. L'application du masque
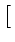
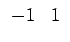
![$ \left.\vphantom{\begin{array}{cc}
-1 & 1\end{array}}\right]$](img714.gif) fournit un résultat compris dans l'intervalle
[- 255, 255]. Sans
renormalisation, il n'est pas possible de représenter correctement
l'ensemble de ces valeurs avec 8 bits. On procède alors à une normalisation
de l'échelle de manière à ramener les valeurs dans l'intervalle de
départ. Dans l'exemple précédent, on appliquera une division par 2
et suivie d'une addition de 128. On pourrait aussi ne considérer que
le module du gradient, ce qui ramène automatiquement le résultat dans
la dynamique initiale.
fournit un résultat compris dans l'intervalle
[- 255, 255]. Sans
renormalisation, il n'est pas possible de représenter correctement
l'ensemble de ces valeurs avec 8 bits. On procède alors à une normalisation
de l'échelle de manière à ramener les valeurs dans l'intervalle de
départ. Dans l'exemple précédent, on appliquera une division par 2
et suivie d'une addition de 128. On pourrait aussi ne considérer que
le module du gradient, ce qui ramène automatiquement le résultat dans
la dynamique initiale.
- Facteurs de normalisation. Pour
des raisons connexes à celles évoquées au point précédent, il n'est
pas toujours utile de considérer le facteur de normalisation correct
de l'opérateur dérivé; on préfère en général procéder à la renormalisation
des valeurs.
Les formes de base effectuent un gradient ligne par ligne ou colonne
par colonne. Les directions horizontales et verticales sont dès lors
privilégiées. Il existe des formes qui permettent de fournir un gradient
aux caractéristiques plus isotropes. Pour y parvenir, ces formes s'étendent
dans les deux directions.
Les filtres de gradient de PREWITT appartiennent
à cette classe d'opérateurs gradient. Ils valent
Figure 6.6:
Image originale, images traitées respectivement par le filtre horizontal
et le filtre vertical de PREWITT.
|
|
La figure montre l'effet des filtres de PREWITT. Le calcul
pratique s'effectue en appliquant successivement une convolution par
la colonne verticale puis par la ligne horizontale, plutôt qu'en traitant
l'image par la matrice carrée. En effet, on sait que
f (x, y) 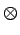
 hxv
hxv 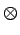 hxh
hxh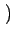 =
= 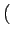 f (x, y)
f (x, y) 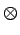 hxv
hxv
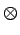 hxv.
Cette astuce algorithmique réduit quelque peu le nombre d'opérations
à effectuer.
hxv.
Cette astuce algorithmique réduit quelque peu le nombre d'opérations
à effectuer.
Les filtres de SOBEL constituent une alternative
aux filtres de PREWITT. Ils s'expriment comme suit
La figure 6.7 montre l'effet des filtres de SOBEL.
Figure 6.7:
Une image originale et les images traitées par application d'un masque
de SOBEL (respectivement horizontal et vertical).
|
|
La comparaison des figures 6.6 et 6.7
montre que les différences entre les images filtrées sont minimes.
Les formes de base comprennent les filtres horizontaux et verticaux
suivants
provenant directement de l'approximation de la dérivée seconde donnée
précédemment.
On peut obtenir un filtre bidimensionnel en combinant les deux expressions
précédentes ou lui préférer un masque de type
qui a un caractère plus isotrope.
La figure 6.8 illustre l'application de
ces différents masques; on y a représenté respectivement l'image originale,
le laplacien horizontal, le laplacien vertical, le laplacien obtenu
avec le masque 6.43 et enfin l'image résultant de
l'application du masque suivant
Figure 6.8:
Illustrations de l'application de masques de dérivée seconde.
|
|
Notes
- ...
suivant6.1
- En toute rigueur, tous les masques sont précédés de facteurs de normalisation.
Nous négligerons parfois ces facteurs car, en pratique, on renormalise
bien souvent le résultat.
Marc Van Droogenbroeck. Tous droits réservés.
2003-09-30
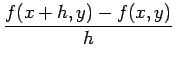
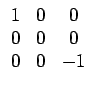
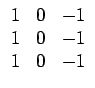
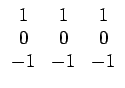

![]()
![]() hxv
hxv ![]() hxh
hxh![]() =
= ![]() f (x, y)
f (x, y) ![]() hxv
hxv![]()
![]() hxv.
Cette astuce algorithmique réduit quelque peu le nombre d'opérations
à effectuer.
hxv.
Cette astuce algorithmique réduit quelque peu le nombre d'opérations
à effectuer.