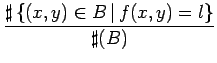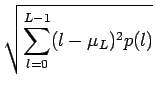Sous-sections
Commençons par définir la notion d'histogramme.
Définition 59
L'histogramme d'une image est la courbe
représentant la fréquence des occurrences des niveaux de gris présents
dans l'image.
Considérons l'image suivante:
| 0 |
0 |
0 |
0 |
0 |
0 |
| 0 |
2 |
1 |
2 |
2 |
2 |
| 2 |
1 |
1 |
1 |
2 |
2 |
| 2 |
1 |
1 |
1 |
2 |
2 |
| 3 |
2 |
1 |
0 |
0 |
0 |
| 3 |
3 |
3 |
3 |
2 |
0 |
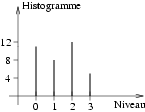
comportant L = 4 niveaux de gris (l = 0, 1, 2, 3). Son histogramme
est représenté à la figure 7.6. Pour le
construire, il suffit de compter le nombre de pixels ayant le niveau
de gris 0, 1, ... et de reporter cette valeur sur le graphique.
On peut également diviser cette valeur par le nombre total de pixels
de l'image pour obtenir la probabilité d'occurrence d'un niveau de
gris. Un exemple d'histogramme pour une image en 256 niveaux de gris
est également donné à la figure 7.7.
Figure 7.6:
Histogramme (non normalisé) d'une image.
|
|
Figure 7.7:
Une image et son histogramme (global car ici B correspond à l'image
entière)
|
|
Définition 60
À partir d'une fenêtre B dans l'image, il est possible de
définir un histogramme local normalisé p(l ) comme suit
p(l )= 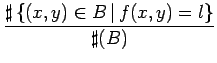 |
(7.3) |
L'histogramme p(l ) représente donc la probabilité d'occurrence
du niveau de gris l parmi les
 (B) pixels de la fenêtre
B. L'histogramme local ainsi défini peut directement servir de
descripteur de texture mais on lui préfère d'autres mesures plus classiques
permettant de le caractériser:
(B) pixels de la fenêtre
B. L'histogramme local ainsi défini peut directement servir de
descripteur de texture mais on lui préfère d'autres mesures plus classiques
permettant de le caractériser:
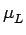 = = 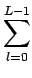 l p(l ) l p(l ) |
(7.4) |
où L est le nombre de niveaux de gris présent dans la fenêtre B.
Cette formule fournit en fait un moyen simple de calculer la moyenne
locale 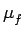 à partir de l'histogramme local. En effet,
on remarquera que
à partir de l'histogramme local. En effet,
on remarquera que
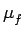 =
= 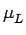 .
.
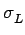 = = 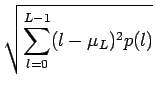 |
(7.5) |
7.2.3.3 Obliquité
7.2.3.4 ``Kurtosis''
Sk = 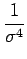 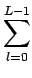 (l - (l - 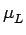 )4 p(l )- 3 )4 p(l )- 3 |
(7.7) |
SE = 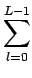 p(l )2 p(l )2 |
(7.8) |
7.2.3.6 Entropie
SH = - 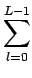 p(l ) log2p(l ) p(l ) log2p(l ) |
(7.9) |
Tous les paramètres qui viennent d'être introduits peuvent être utilisés
comme descripteurs de la texture. Cependant, il n'existe pas de descripteur
idéal. En raison du faible pouvoir discriminant des ces paramètres,
il est nécessaire de combiner plusieurs descripteurs.
Marc Van Droogenbroeck. Tous droits réservés.
2003-09-30