 |
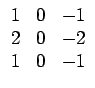 |
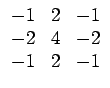 |
| Laws 1 | Laws 2 | Laws 3 |
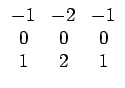 |
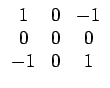 |
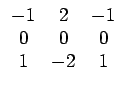 |
| Laws 4 | Laws 5 | Laws 6 |
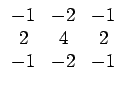 |
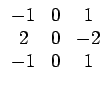 |
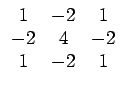 |
| Laws 7 | Laws 8 | Laws 9 |
Dans l'étude des textures, LAWS a introduit différentes mesures permettant de caractériser l'énergie d'une texture.
Ces mesures déterminent les propriétés d'une texture à partir d'une estimation du profil de niveaux de gris en termes de contours, de tacheté (spot), d'ondulation et de vague. Les mesures sont dérivées de trois vecteurs simples: L3 = (1, 2, 1) qui effectue la moyenne, E3 = (- 1, 0, 1) qui détecte les contours et S3 = (- 1, 2, - 1) qui correspond à la dérivée seconde. Par convolution de ces vecteurs (symétriques) par eux-mêmes et entre eux, LAWS a introduit 9 masques de convolution:
 |
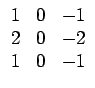 |
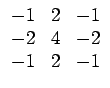 |
| Laws 1 | Laws 2 | Laws 3 |
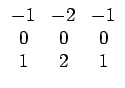 |
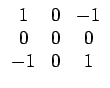 |
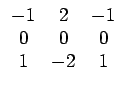 |
| Laws 4 | Laws 5 | Laws 6 |
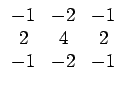 |
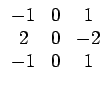 |
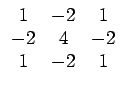 |
| Laws 7 | Laws 8 | Laws 9 |
De même, il est possible de générer des vecteurs de taille 5:
| L5 | = | (1, 4, 6, 4, 1) | (7.25) |
| E5 | = | (- 1, - 2, 0, 2, 1) | (7.26) |
| S5 | = | (- 1, 0, 2, 0, - 1) | (7.27) |
| R5 | = | (1, - 4, 6, - 4, 1) | (7.28) |
| W5 | = | (- 1, 2, 0, - 2, - 1) | (7.29) |
L5T×S5 = 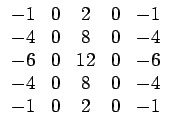 |
(7.30) |
La convolution d'une texture au moyen des masques de LAWS suivie d'un calcul d'une statistique d'énergie permet de dériver une information intéressante pour la description ou la discrimination de textures. La figure 7.9 montre des exemples de textures traitées par les masques de LAWS.
|
On remarque que le pouvoir discriminant des masques n'est pas identique. Par contre, la combinaison des résultats est à même de fournir une information suffisamment riche pour discriminer et identifier les textures. La combinaison des critères est bien souvent le seul moyen efficace d'aboutir. Il convient alors d'attirer l'attention sur le fait que les mesures n'ont pas toutes les mêmes dimensions physiques, certains sont des moyennes, d'autres des énergies ou des mesures adimensionnelles; leur combinaison est alors hasardeuse.