8.1 Généralités

L'acquisition d'une image s'accompagne souvent d'une distorsion ou d'une certaine dégradation. On peut songer par exemple à un éclairage non uniforme, à des poussières sur une lentille ou encore à un flou créé par un mouvement lors de l'acquisition. Il n'y a dès lors pas d'autre solution que de chercher à corriger les défauts par un procédé algorithmique.

On distingue deux grandes familles de procédés de correction des défauts:

le rehaussement, qui consiste à donner à l'image un aspect visuellement correct, et
la restauration, qui cherche à rétablir la valeur exacte des pixels.

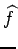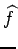Dans les deux cas, on part à la recherche d'une estimation $\widehat{{f}}$ (x, y) de l'image f (x, y) qui soit visuellement ou analytiquement intéressante, c'est-à-dire qu'elle minimise une fonction d'erreur e(x, y) = e( $\widehat{{f}}$ , f ). Comme il n'existe pas de fonction d'erreur capable de modéliser la perception visuelle, le rehaussement est principalement de nature empirique. Ce n'est pas le cas de la restauration qui s'appuie sur une définition précise de la fonction d'erreur. Il s'agit par exemple de minimiser l'erreur quadratique moyenne

e(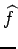 $\displaystyle \widehat{{f}}$ , f )= 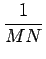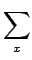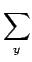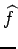$\displaystyle {\frac{{1}}{{MN}}}$ $\displaystyle \sum_{{x}}^{}$ $\displaystyle \sum_{{y}}^{}$ ( $\displaystyle \widehat{{f}}$ (x, y) - f (x, y))²

(8.1)

Cette fonction est un choix commun car

la fonction se calcule aisément,
elle est différentiable, et
elle correspond à l'énergie de l'erreur. Par la relation de PARSEVAL, l'énergie correspond également à l'énergie de la transformée de FOURIER.

La figure 8.1 illustre la marge de manoeuvre dont on dispose pour du rehaussement par rapport à la restauration. L'image 8.1(b) a été obtenue en divisant, par division entière, l'image originale par 5 puis en multipliant toutes les valeurs par 5; c'est en fait un arrondi au plus petit multiple de 5 inférieur à chaque valeur. Les images (c) et (d) résultent d'approximations plus grossières encore.

Figure 8.1: Seuil de visibilité pour une opération d'arrondi.


(a) Image originale f	(b) Arrondi à 5


(c) Arrondi à 10	(d) Arrondi à 20

On voit clairement qu'un arrondi à 10 n'est pas gênant, ce qui revient à dire que les trois bits de poids faible sont peu visibles. Au-delà, l'erreur de quantification devient perceptible.