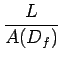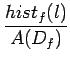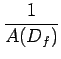Sous-sections
Soit o(x, y) l'image de sortie. On cherche à déterminer le lien
entre l'histogramme
histo(l ) de cette
image avec celui de l'image d'entrée f. D'une manière générale,
pour une valeur lo de l'image de sortie, il existe une fonction
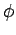 telle que
telle que
lo = 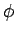 (lf) (lf) |
(8.6) |
Si cette fonction admet un inverse, ce qui est le cas si l'on impose
la croissance et l'existence d'une dérivée non nulle,
lf = 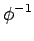 (lo) (lo) |
(8.7) |
Si l'on interprète l'histogramme comme une densité de probabilité,
on arrive à une égalité entre les ``masses'' que sont
| histo(lo)dlo = histf(lf)dlf |
(8.8) |
Dès lors,
| histo(lo) |
= |
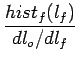 |
(8.9) |
| |
= |
 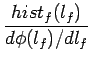 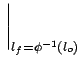 |
(8.10) |
et donc
histo(l )= 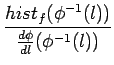 |
(8.11) |
Considérons la fonction 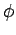 suivante
suivante
lo = 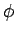 (lf) = (lf) = 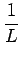 (lf)2 (lf)2 |
(8.12) |
d'où également
lf = 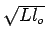 . Par application de la formule 8.11,
. Par application de la formule 8.11,
histo(l )= 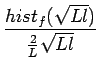 = = 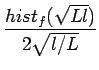 |
(8.13) |
Dans une image réelle, tous les niveaux ne sont pas présents avec
une même occurrence. Il en résulte donc des disparités dans l'histogramme.
L'égalisation de l'histogramme
d'une image est une méthode courante de rehaussement. Elle vise à
assurer une distribution homogène des valeurs dans la totalité de
la plage dynamique des valeurs possibles. Il s'agit donc d'une distorsion
de l'échelle des valeurs. Formellement, pour toute valeur l de
l'histogramme résultat, le nombre de pixels devrait valoir
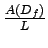 ,
où
A(Df) représente l'aire du support de définition de la
fonction f. L'équation 8.11 devient
donc
,
où
A(Df) représente l'aire du support de définition de la
fonction f. L'équation 8.11 devient
donc
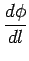 (l )= (l )= 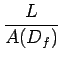 histf(l ) histf(l ) |
(8.14) |
Par intégration des membres de cette dernière relation,
Comme on peut estimer la probabilité d'un niveau par le rapport de
la fréquence à l'aire du domaine de définition de la fonction
p(l )= 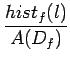 |
(8.16) |
De plus, la fonction de répartition F est l'intégrale cumulée des
probabilités
F(l )= 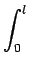 p(k)dk = p(k)dk = 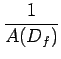 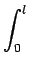 histf(k)dk histf(k)dk |
(8.17) |
Dès lors,
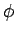 (l )= LF(l ) (l )= LF(l ) |
(8.18) |
Autrement dit, l'image o(x, y) traitée par la fonction qui effectue
une égalisation de l'histogramme vaut
| o(x, y) = LF(f (x, y)) |
(8.19) |
En raison des valeurs quantifiées, l'égalisation de l'histogramme
peut fournir un histogramme non uniforme. Il ne faut pas s'en étonner.
Ce phénomène est illustré à la figure 8.4.
Marc Van Droogenbroeck. Tous droits réservés.
2003-09-30
![]() telle que
telle que 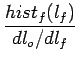
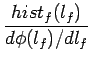
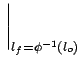
![]() suivante
suivante 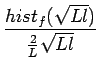 =
= 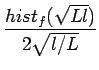
![]() ,
où
A(Df) représente l'aire du support de définition de la
fonction f. L'équation 8.11 devient
donc
,
où
A(Df) représente l'aire du support de définition de la
fonction f. L'équation 8.11 devient
donc 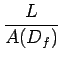 histf(l )
histf(l )