Sous-sections
Le filtre de WIENER
est un filtre linéaire souvent utilisé pour la réduction de bruit.
Dès lors, dans cette section, nous considérons que l'image originale
n'a subi comme dégradation que l'ajout d'un bruit aléatoire. Afin
de simplifier les développements mathématiques, nous nous limiterons
au cas d'une fonction à une dimension. Ce résultat sera alors aisément
généralisé à deux dimensions.
La figure 8.10 illustre le modèle que nous
allons utiliser. w(t) représente la fonction dégradée par l'ajout
du bruit n(t) tandis que
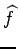 (t) représente la fonction
restaurée au départ de w(t) par une convolution avec le filtre
de réponse impulsionnelle h(t). Idéalement, nous aimerions obtenir
(t) représente la fonction
restaurée au départ de w(t) par une convolution avec le filtre
de réponse impulsionnelle h(t). Idéalement, nous aimerions obtenir
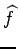 (t) = f (t) mais en général, un filtre linéaire n'est pas
assez puissant pour retrouver le signal de départ f (t) de manière
exacte. Le but est alors de déterminer la fonction h(t) qui rende
(t) = f (t) mais en général, un filtre linéaire n'est pas
assez puissant pour retrouver le signal de départ f (t) de manière
exacte. Le but est alors de déterminer la fonction h(t) qui rende
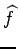 (t) le plus proche de f (t).
(t) le plus proche de f (t).
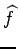 (t) est
appelée estimation de f (t).
(t) est
appelée estimation de f (t).
Figure 8.10:
Modèle utilisé pour le filtre de WIENER.
|
|
Dans cette étude, nous ferons l'hypothèse que les signaux f (t)
et n(t) sont des processus aléatoires ergodiques et de densité
spectrale de puissance
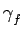 (f ) et
(f ) et
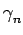 (f ) connues.
(f ) connues.
Avant de déterminer le filtre optimal, que l'on notera ho(t),
il est nécessaire de définir un critère d'optimalité. Vu que
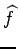 (t) = f (t)
n'est pas réalisable, nous allons utiliser comme critère l'erreur
quadratique moyenne.
(t) = f (t)
n'est pas réalisable, nous allons utiliser comme critère l'erreur
quadratique moyenne.
Quelque soit l'expression de h(t), nous obtiendrons en sortie un
signal
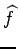 (t) en réponse à f (t). Le signal d'erreur
à la sortie du filtre est défini par
(t) en réponse à f (t). Le signal d'erreur
à la sortie du filtre est défini par
e(t) = f (t) - 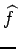 (t) (t) |
(8.33) |
qui mesure l'écart instantané entre la fonction restaurée et la fonction
idéale. Comme mesure de l'erreur moyenne, nous utiliserons l'erreur
quadratique moyenne définie par
Ici, l'espérance mathématique peut se calculer comme une intégrale
sur le temps vu que les processus sont supposés ergodiques. On remarquera
que l'erreur quadratique moyenne pénalise plus les grands écarts entre
f (t) et
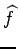 (t) comparés aux faibles écarts, ce qui constitue
un critère tout à fait satisfaisant.
(t) comparés aux faibles écarts, ce qui constitue
un critère tout à fait satisfaisant.
Le problème se ramène à présent à déterminer une fonction h(t)
qui minimise l'erreur quadratique moyenne
E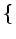 e2(t)
e2(t) ,
qui est un nombre. Il s'agit en fait de la minimisation d'une fonctionnelle
qui relève du calcul des variations. Nous allons suivre la démarche
suivante:
,
qui est un nombre. Il s'agit en fait de la minimisation d'une fonctionnelle
qui relève du calcul des variations. Nous allons suivre la démarche
suivante:
- exprimer l'erreur quadratique moyenne en terme de la fonction h(t),
- déterminer l'expression optimale ho(t) en terme des densités
spectrales de puissance connues, et finalement
- calculer la valeur de l'erreur quadratique moyenne lorsque le filtre
optimal ho(t) est utilisé.
Nous commençons par développer l'erreur quadratique moyenne de la
manière suivante
E e2(t) e2(t) |
= |
E f2(t) - 2f (t) f2(t) - 2f (t)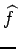 (t) + (t) + 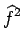 (t) (t) |
(8.35) |
| |
= |
E f2(t) f2(t)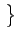 -2E -2E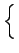 f (t) f (t)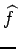 (t) (t)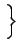 + E + E 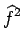 (t) (t) |
(8.36) |
| |
= |
T1 + T2 + T3 |
(8.37) |
où
T1, T2 et T3 sont trois termes que l'on va traiter
séparément. T1 se ramène à
T1 = E f2(t) f2(t) = =  f2(t)dt = f2(t)dt = 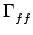  0 0 |
(8.38) |
où
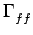
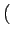 0
0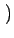 est la fonction d'autocorrélation de
f (t) évalué en 0. T1 correspond donc à la puissance du
signal f (t). Le second membre T2 peut s'écrire
est la fonction d'autocorrélation de
f (t) évalué en 0. T1 correspond donc à la puissance du
signal f (t). Le second membre T2 peut s'écrire
T2 = - 2E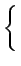 f (t) f (t) h( h( )w(t - )w(t -  )d )d 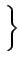 |
(8.39) |
où nous avons remplacé
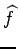 (t) par le produit de convolution
entre w(t) et h(t). Vu que l'espérance mathématique est une
intégrale sur le temps, il est possible d'inverser l'ordre d'intégration:
(t) par le produit de convolution
entre w(t) et h(t). Vu que l'espérance mathématique est une
intégrale sur le temps, il est possible d'inverser l'ordre d'intégration:
| T2 |
= |
-2 h( h( )E )E f (t)w(t - f (t)w(t -  ) ) d d |
(8.40) |
| |
= |
-2 h( h( ) )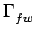 ( ( )d )d |
(8.41) |
où
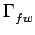 (
(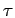 ) est la fonction d'intercorrélation
de f (t) et w(t). Le troisième terme T3 peut être traité
d'une manière similaire
) est la fonction d'intercorrélation
de f (t) et w(t). Le troisième terme T3 peut être traité
d'une manière similaire
| T3 |
= |
E  h( h( )w(t - )w(t -  )d )d  h(u)w(t - u)du h(u)w(t - u)du |
(8.42) |
| |
= |
  h( h( )h(u)E )h(u)E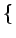 w(t - w(t -  )w(t - u) )w(t - u)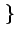 d d du du |
(8.43) |
Si l'on écrit le changement de variables v = t - u dans l'espérance,
nous obtenons
E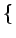 w(t - w(t -  )w(t - u) )w(t - u)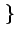 = E = E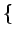 w(v + u - w(v + u -  )w(v) )w(v)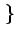 = = 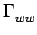 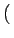 u - u -  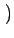 |
(8.44) |
et donc
T3 =   h( h( )h(u) )h(u)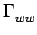 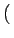 u - u -  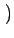 d d du du |
(8.45) |
Dès lors, l'erreur quadratique moyenne peut maintenant s'écrire
E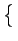 e2(t) e2(t)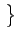 = = 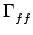 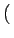 0 0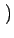 -2 -2 h( h( ) )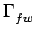 ( ( )d )d + +   h( h( )h(u) )h(u)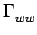 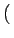 u - u -  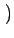 d d du du |
(8.46) |
Étant donné que les fonctions d'autocorrélation et d'intercorrélation
sont connues, on remarque que l'erreur quadratique moyenne est bien
une fonction de h(t).
Considérons le filtre optimal ho(t). Tout autre filtre peut
s'écrire comme
| h(t) = ho(t) + g(t) |
(8.47) |
où h(t) est une réponse impulsionnelle arbitraire sous-optimale
et g(t) est définie comme l'écart instantané entre le filtre optimal
ho(t) et le filtre sous-optimal h(t). Si nous introduisons
cette dernière expression dans l'expression de l'erreur quadratique
moyenne, nous obtenons
E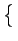 e2(t) e2(t)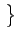 |
= |
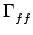 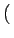 0 0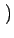 -2 -2 (ho( (ho( ) + g( ) + g( )) ))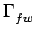 ( ( )d )d |
(8.48) |
| |
|
+   (ho( (ho( ) + g( ) + g( ))(ho(u) + g(u)) ))(ho(u) + g(u))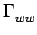  u - u -   d d du du |
(8.49) |
ce qui peut s'écrire sous la forme de sept termes:
E e2(t) e2(t) |
= |
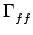  0 0 -2 -2 ho( ho( ) )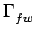 ( ( )d )d |
(8.50) |
| |
|
+   ho( ho( )ho(u) )ho(u)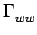  u - u -   d d du du |
(8.51) |
| |
|
+   ho( ho( )g(u) )g(u)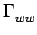 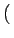 u - u -  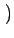 d d du du |
(8.52) |
| |
|
+   ho(u)g( ho(u)g( ) )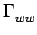 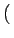 u - u -  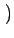 d d du du |
(8.53) |
| |
|
-2 g( g( ) )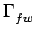 ( ( )d )d + +   g( g( )g(u) )g(u)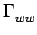 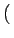 u - u -  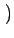 d d du du |
(8.54) |
Les trois premiers termes correspondent à l'erreur quadratique moyenne
dans le cas du filtre optimal ho(t). On notera cette valeur
Eo. Vu que la fonction d'autocorrélation
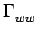
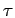
 est paire, les troisième et quatrième termes sont égaux. Nous pouvons
alors les combiner avec le sixième terme pour obtenir
est paire, les troisième et quatrième termes sont égaux. Nous pouvons
alors les combiner avec le sixième terme pour obtenir
E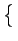 e2(t) e2(t)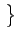 |
= |
Eo +2 g(u) g(u)  ho( ho( ) )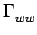  u - u -   d d - - 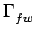 (u) (u)![$\displaystyle \left.\vphantom{\int_{-\infty}^{+\infty}h_{o}(\tau)\Gamma _{ww}\left(u-\tau\right)d\tau-\Gamma _{fw}(u)}\right]$](img910.gif) du du |
(8.55) |
| |
|
+   g( g( )g(u) )g(u)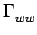  u - u -   d d du du |
(8.56) |
| |
= |
Eo + T4 + T5 |
(8.57) |
où T4 et T5 sont à nouveau deux termes que nous allons
traiter séparément. Montrons tout d'abord que le terme T5 est
toujours positif. En exprimant la fonction d'autocorrélation par une
intégrale, nous obtenons
| T5 |
= |
  g( g( )g(u) )g(u) w(t - w(t -  )w(t - u)dtd )w(t - u)dtd du du |
(8.58) |
| |
= |
  w(t - u)g(u)du w(t - u)g(u)du g( g( )w(t - )w(t -  )d )d dt dt |
(8.59) |
Si l'on définit
z(t) = g(t) 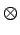 w(t), ce terme vaut
w(t), ce terme vaut
T5 =  z2(t)dt z2(t)dt 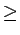 0 0 |
(8.60) |
qui ne peut jamais être négatif. Remarquons que cette valeur est indépendante
de l'expression du filtre idéal ho(t).
Retournons à présent à l'expression de l'erreur quadratique moyenne:
E e2(t) e2(t) = Eo +2 = Eo +2 g(u) g(u)  ho( ho( ) )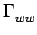 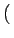 u - u -  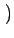 d d - - 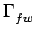 ( ( ) )![$\displaystyle \left.\vphantom{\int_{-\infty}^{+\infty}h_{o}(\tau)\Gamma _{ww}\left(u-\tau\right)d\tau-\Gamma _{fw}(\tau)}\right]$](img912.gif) du + T5 du + T5 |
(8.61) |
Nous allons à présent établir la condition qui assure que Eo
soit la plus petite erreur quadratique moyenne que l'on puisse obtenir.
Un moyen est de faire en sorte que le terme entre crochets soit nul
pour toute valeur de u. Il faut alors assurer qu'il s'agit d'une
condition nécessaire et suffisante pour optimiser le filtre. La condition
est tout d'abord nécessaire. En effet, si le terme entre crochets
était non nul pour certaines valeurs de u, le terme T4 pourrait
prendre des valeurs fortement négatives vu que g(u) est une fonction
totalement arbitraire. Il en découlerait que
E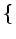 e2(t)
e2(t)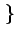 pourrait être inférieure à E0, ce qui violerait notre définition.
Nous obtenons donc une condition nécessaire pour que le filtre ho(t)
soit optimal:
pourrait être inférieure à E0, ce qui violerait notre définition.
Nous obtenons donc une condition nécessaire pour que le filtre ho(t)
soit optimal:
Cette condition est de plus suffisante. En effet, il suffit qu'elle
soit vérifiée pour que le terme T4 disparaisse et dès lors
E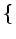 e2(t)
e2(t)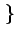 sera toujours supérieure ou égale à Eo, vu que
T5
sera toujours supérieure ou égale à Eo, vu que
T5 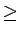 0.
0.
Pour les systèmes linéaires, il est aisé de montrer que
où
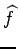 (t) et w(t) sont respectivement la sortie et l'entrée
du système caractérisé par h(t). Étant donnée la condition
d'optimalité sur ho(t), nous pouvons écrire
Cette seconde égalité montre que le filtre de WIENER rend
l'intercorrélation entre le signal idéal et le signal dégradé égal
à l'intercorrélation entre le signal dégradé et le signal restauré.
En prenant la transformée de FOURIER de chacun des membres
de l'égalité, nous obtenons
(t) et w(t) sont respectivement la sortie et l'entrée
du système caractérisé par h(t). Étant donnée la condition
d'optimalité sur ho(t), nous pouvons écrire
Cette seconde égalité montre que le filtre de WIENER rend
l'intercorrélation entre le signal idéal et le signal dégradé égal
à l'intercorrélation entre le signal dégradé et le signal restauré.
En prenant la transformée de FOURIER de chacun des membres
de l'égalité, nous obtenons
et dès lors,
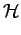 o(f )= o(f )= 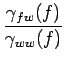 |
(8.65) |
qui correspond donc à l'expression fréquentielle du filtre optimal
en fonction des données du problème.
Tel quel, on éprouve du mal à interpréter l'expression fréquentielle
du filtre optimal. Ce n'est plus le cas lorsque l'on fait l'hypothèse
supplémentaire que les signaux f (t) et n(t) sont indépendants.
Dans ce cas, nous pouvons écrire
E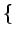 f (t) n(t) f (t) n(t)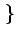 = E = E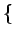 f (t) f (t) E E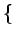 n(t) n(t) |
(8.66) |
Nous pouvons alors transformer le numérateur de
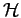 o(f )
de la manière suivante
o(f )
de la manière suivante
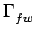 ( ( ) = E ) = E w(t) f (t + w(t) f (t +  ) ) = E = E![$\displaystyle \left\{\vphantom{ \left[f(t)+n(t)\right]\, f(t+\tau)}\right.$](img927.gif)  f (t) + n(t) f (t) + n(t)![$\displaystyle \left.\vphantom{f(t)+n(t)}\right]$](img929.gif) f (t + f (t +  ) )![$\displaystyle \left.\vphantom{ \left[f(t)+n(t)\right]\, f(t+\tau)}\right\}$](img930.gif) |
(8.67) |
ou encore
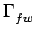 ( ( ) = ) = 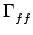    + E + E n(t) n(t) E E f (t + z) f (t + z) = = 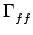   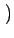 + +  n(t) dt n(t) dt  f (t + f (t +  ) dt ) dt |
(8.68) |
et finalement
où
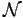 (0) et
(0) et
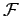 (0) sont respectivement les
transformées de FOURIER de n(t) et f (t) évaluée en
0. Un raisonnement similaire peut être appliqué au dénominateur de
(0) sont respectivement les
transformées de FOURIER de n(t) et f (t) évaluée en
0. Un raisonnement similaire peut être appliqué au dénominateur de
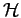 o(f ):
o(f ):
On peut à présent réécrire l'expression fréquentielle du filtre optimal:
où nous n'avons pas considéré la composante continue. Remarquons qu'en
l'absence de bruit, la fonction de transfert du filtre optimal est
égale à 1. Cette dernière expression donne le filtre optimal en termes
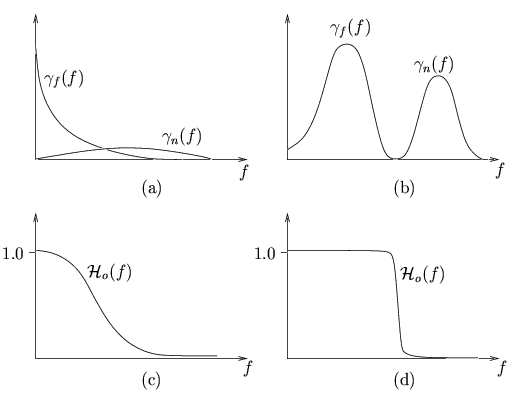
des différentes densités spectrales de puissance connues. La figure
8.11 montre des exemples de filtres de WIENER
dans des cas typiques.
Figure 8.11:
Illustration du filtre de WIENER. (a) et (c): signal utile
passe-bas et bruit s'étalant sur toute la gamme de fréquences. (b)
et (d): signal utile et bruit du type passe-bande.
|
|
Marc Van Droogenbroeck. Tous droits réservés.
2003-09-30
![]() (t) représente la fonction
restaurée au départ de w(t) par une convolution avec le filtre
de réponse impulsionnelle h(t). Idéalement, nous aimerions obtenir
(t) représente la fonction
restaurée au départ de w(t) par une convolution avec le filtre
de réponse impulsionnelle h(t). Idéalement, nous aimerions obtenir
![]() (t) = f (t) mais en général, un filtre linéaire n'est pas
assez puissant pour retrouver le signal de départ f (t) de manière
exacte. Le but est alors de déterminer la fonction h(t) qui rende
(t) = f (t) mais en général, un filtre linéaire n'est pas
assez puissant pour retrouver le signal de départ f (t) de manière
exacte. Le but est alors de déterminer la fonction h(t) qui rende
![]() (t) le plus proche de f (t).
(t) le plus proche de f (t).
![]() (t) est
appelée estimation de f (t).
(t) est
appelée estimation de f (t).
![]() (f ) et
(f ) et
![]() (f ) connues.
(f ) connues.
![]() (t) = f (t)
n'est pas réalisable, nous allons utiliser comme critère l'erreur
quadratique moyenne.
(t) = f (t)
n'est pas réalisable, nous allons utiliser comme critère l'erreur
quadratique moyenne.
![]() (t) en réponse à f (t). Le signal d'erreur
à la sortie du filtre est défini par
(t) en réponse à f (t). Le signal d'erreur
à la sortie du filtre est défini par![]() e2(t)
e2(t)![]() ,
qui est un nombre. Il s'agit en fait de la minimisation d'une fonctionnelle
qui relève du calcul des variations. Nous allons suivre la démarche
suivante:
,
qui est un nombre. Il s'agit en fait de la minimisation d'une fonctionnelle
qui relève du calcul des variations. Nous allons suivre la démarche
suivante:
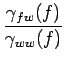
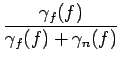 f
f