Ainsi que l'on vient de le voir, le filtrage de WIENER ne permet que de restaurer des images qui ont été dégradées par l'ajout d'un bruit aléatoire. Nous allons voir qu'il est possible de combiner le filtrage de WIENER avec un procédé de déconvolution.
Considérons le schéma de la figure 8.12.
Comme pour le filtrage de WIENER, nous allons réaliser le
raisonnement pour le cas à une dimension. La fonction idéale est ici
dégradée par convolution avec un filtre dont la fonction de transfert
est
![]() (f ) et par l'ajout d'un bruit n(t). La fonction
dégradée est toujours notée w(t).
(f ) et par l'ajout d'un bruit n(t). La fonction
dégradée est toujours notée w(t).
Avant d'appliquer la technique du filtrage de WIENER, il
est nécessaire de réaliser la déconvolution par un filtre dont la
fonction de transfert est égal à l'inverse de la fonction de transfert
![]() (f ). Le filtre global de restauration est obtenu par
combinaison du filtre de déconvolution et du filtre de WIENER.
Vu que le filtre de déconvolution est connu, il reste simplement à
déterminer la fonction de transfert
(f ). Le filtre global de restauration est obtenu par
combinaison du filtre de déconvolution et du filtre de WIENER.
Vu que le filtre de déconvolution est connu, il reste simplement à
déterminer la fonction de transfert
![]() o(f ) du filtre
de WIENER avant de combiner les deux filtres.
o(f ) du filtre
de WIENER avant de combiner les deux filtres.
Calculons la transformée de FOURIER du signal dégradé
| (8.72) |
| = | 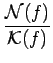 |
(8.73) | |
| = | (8.74) |
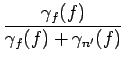 |
(8.75) |
| = | 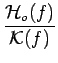 |
(8.76) | |
| = | 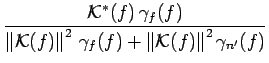 |
(8.77) |
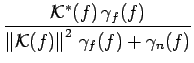 |
(8.78) |
La déconvolution de WIENER peut aisément être adaptée aux
cas des images à deux dimensions. Si l'on note
![]() (u, v) la
densité spectrale de puissance de l'image f (x, y),
(u, v) la
densité spectrale de puissance de l'image f (x, y),
![]() (u, v)
celle du bruit aléatoire additionnel et
(u, v)
celle du bruit aléatoire additionnel et
![]() (u, v) la fonction
de transfert du filtre ayant dégradé l'image originale, la déconvolution
de WIENER se caractérise par le filtre de déconvolution suivant
(u, v) la fonction
de transfert du filtre ayant dégradé l'image originale, la déconvolution
de WIENER se caractérise par le filtre de déconvolution suivant
| = | 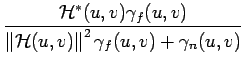 |
(8.79) | |
| = | 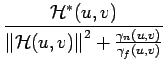 |
(8.80) |