Table des matières of 9.1.1 Description linéique de la forme

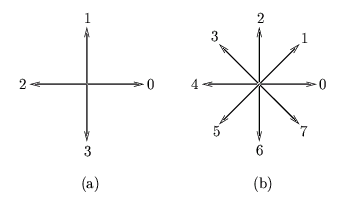
Le codage en chaîne (run-length coding en anglais) est une description fort utilisée en codage des contours. Elle consiste à définir un jeu de directions (cf. figure 9.1) et à suivre les points de contours de proche en proche jusqu'à revenir au point de départ. Un contour se définit alors comme une structure contenant les coordonnées du point de départ et une liste de directions à suivre.

**Figure 9.1:** Directions en 4-connexité (a) et en 8-connexité (b).

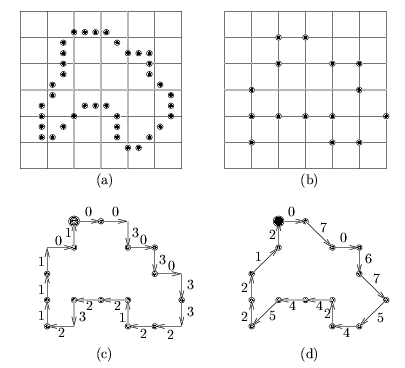
La figure 9.2 montre des exemples de codage en chaîne en 4 et 8-connexité. Le codage en chaîne en 8-connexité fournit (x₁, y₁), 070675424452212. Le codage en 8-connexité est toujours plus court que le codage en 4-connexité mais il fait intervenir plus de directions distinctes.

**Figure 9.2:** (a) Un contour, (b) contour après échantillonnage sur une grille, (c) codage en chaîne en 4-connexité et (d) codage en chaîne en 8-connexité.

Un problème typique du codage en chaîne intervient lors de la présence de points de rebroussement. On remarque alors qu'un même point de contour est décrit plusieurs fois. Ce phénomène est illustré à la figure 9.3.

**Figure 9.3:** Contour avec des points de rebroussement.

9.1.1.2 Approximation polygonale

En général, on cherche à approcher au mieux la forme d'un contour avec un minimum de côtés. Le problème d'approximation polygonale d'un contour n'est pas trivial en tant que tel et l'on se heurterait rapidement à des temps de calcul excessif si on procède itérativement. Néanmoins, il existe des techniques satisfaisante pour le traitement d'images.

La figure 9.4 montre les étapes d'un procédé d'approximation polygonale d'un contour. On détermine tout d'abord la plus longue corde qu'il est possible de placer à l'intérieur de l'objet; les deux extrémités de cette corde correspondent à deux sommets du quadrilatère d'approximation. Pour trouver les autres sommets, on abaisse les plus longues perpendiculaires de part et d'autre de la corde. L'approximation peut être améliorée en ajoutant des sommets en abaissant les plus longues perpendiculaires sur chaque côté. La technique d'approximation consiste à ajouter des côtés jusqu'au moment où un critère d'arrêt est respecté, par exemple un écart surfacique entre la forme originale et son approximation inférieur à un certain pourcentage.

**Figure 9.4:** Approximation polygonale d'un contour.

9.1.1.3 Descripteur de FOURIER

Un contour est constitué d'une série de coordonnées de type (x_i, y_i) mais une description curviligne conviendrait puisqu'il ne s'agit jamais que d'un objet unidimensionnel parcourant un espace de dimension plus élevée. Partant de ce principe, on peut considérer une représentation sous forme de nombres complexes.

Soit une série de N points de contours dont les coordonnées sont représentées sous forme complexe, tels que représentés à la figure 9.5.

**Figure 9.5:** Représentation d'un contour comme une séquence de points complexes.

$\displaystyle \mathcal {S}$ [u] = $\displaystyle {\frac{{1}}{{N}}}$ $\displaystyle \sum_{{n=0}}^{{N-1}}$ s[n]e^-2jun/N

(9.2)

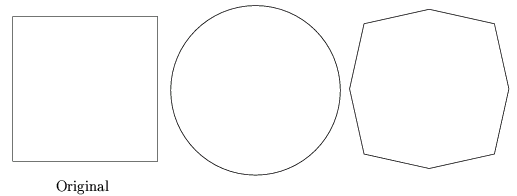
On peut approximer un contour en sélectionnant un certain nombre de descripteurs de FOURIER. La figure 9.6 illustre les approximations successives qui en découlent.

**Figure 9.6:** Forme originale et approximations du contour au moyen d'un nombre restreint de descripteurs de FOURIER.

9.1.1 Description linéique de la forme

9.1.1.1 Le codage en chaîne

9.1.1.2 Approximation polygonale

9.1.1.3 Descripteur de FOURIER