Table des matières of 9.1.3 Le squelette morphologique comme descripteur par éléments de surface

9.1.3 Le squelette morphologique comme descripteur par éléments de surface

Nous avons étudié précédemment des opérateurs morphologiques qui transforment un ensemble en un autre ensemble. Dans la mesure où la morphologie interprète une image en termes d'objets, il est licite de se demander s'il n'existe pas une opération qui est capable de décrire un objet par une série d'ensembles.

Une description en termes d'objets a plusieurs objectifs: interprétation automatique d'images, modélisation de matériau (séparation de phase), reconnaissance de formes, etc. Une description valable d'une scène intègre nécessairement une approche hiérarchique ou multirésolution des objets mais avant de travailler valablement avec des objets de résolution variable, il faudra définir le concept de taille morphologique. Ainsi tant pour le codage que pour le traitement d'objets, il est préférable de traiter en premier lieu les grands ensembles puis de passer successivement aux détails fins. La squelettisation offre une approche intéressante à plusieurs degrés de précision.

9.1.3.1 Définition intuitive du squelette

Considérons un ensemble continu X et sa frontière $\partial$ (X); un point x de X appartiendra au squelette de X, noté S(X), s'il existe un disque centré en x inclus dans X et touchant $\partial$ (X) en deux points au moins. Plus intuitivement le squelette peut être défini comme le lieu des centres des boules maximales B contenues dans X (voir figure 9.8 pour quelques exemples de squelettes). Ces deux définitions ne sont pas tout à fait équivalentes mais elles ont la même fermeture topologique dans $\mathbb {R}$ ².

**Figure 9.8:** Exemple de squelettes de plusieurs ensembles.

L'opérateur issu de cette approche intuitive est défini par les propriétés suivantes:

le résultat est large d'un pixel,
le squelette passe par le milieu des objets, et
l'opérateur de squelettisation préserve la topologie de l'objet.

Nous fournissons plus loin une définition mieux adaptée au cas d'ensembles discrétisés ( $\subseteq$ $\mathbb {Z}$ ²) -la difficulté apparente est comment définir une boule maximale sur une grille d'échantillonnage-, faisant intervenir des érosions et des ouvertures. En fait, on cherche à définir le squelette d'un ensemble discret. Cette définition n'est pas évidente car la boule maximale n'a pas d'équivalent sur une grille d'échantillonnage. Il y a donc plusieurs approches, comme le laisse entrevoir l'illustration de la figure 9.9.

**Figure 9.9:** Que vaut le squelette de X? Idéalement, il se situe au milieu. En pratique, en haut ou en bas.

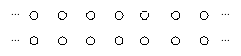
Plus généralement, la définition pratique du squelette dans le cas d'objets définis sur une grille d'échantillonnage pose plusieurs problèmes:

comment définir une boule sur une grille d'échantillonnage?
comment associer une notion pratique de taille à une boule?
faut-il garantir la préservation du nombre de connexité lors de la squelettisation?
l'information fournie par le squelette (c'est-à-dire positions et rayons des boules) est-elle suffisante ou surabondante?

9.1.3.2 Propriétés d'une transformée par squelette

Si la squelettisation (opérateur de X $\rightarrow$ S(X)) respecte les deux premiers principes de toute transformation morphologique, le respect de la continuité n'est pas nécessairement assuré. Par exemple, le squelette d'un polygone régulier est constitué de segments de droite joignant son centre aux sommets; lorsque, par un passage à la limite, on fait tendre le nombre de côtés vers l'infini (cercle), le squelette devient pratiquement équivalent au polygone alors que le squelette d'un cercle se réduit à son centre. La connaissance locale exige aussi quelques précautions.

Citons les propriétés algébriques suivantes.

Propriété 62 La squelettisation est une opération ni croissante ni décroissante. En effet, X $\subseteq$ Y n'entraîne généralement pas que S(X) $\subseteq$ S(Y) ou S(Y) $\subseteq$ S(X).

Propriété 63 La squelettisation est une opération anti-extensive: S(X) $\subseteq$ X.

Propriété 64 La squelettisation est une transformation idempotente: S(S(X)) = S(X).

À cette réflexion, on peut déjà deviner que le squelette est lié à l'ouverture morphologique par des éléments structurants de plusieurs tailles différentes.

Mais avant de fournir l'expression analytique du squelette, nous introduisons le concept de taille morphologique. C'est aussi l'occasion de présenter les filtres multirésolution.

9.1.3.3 Préliminaires: la taille morphologique et les filtres multirésolution

9.1.3.3.1 Taille morphologique.

Définition 65 Soit B un élément structurant dont la taille est fixée arbitrairement à . On définit un espace continu d'ensembles par

rB = {rb| b $\displaystyle \in$ B} r $\displaystyle \geq$ 0

(9.3)

où r est un paramètre continu. L'objet rB a la même forme que B à condition de prendre un ensemble B connexe et borné.

9.1.3.3.2 Homothétie d'un ensemble discret.

La définition précédente ne convient pas du tout pour le cas d'un ensemble discrétisé^9.1. En effet, si B est un carré de 2x2 pixels, alors 2B est composé uniquement des sommets d'un carré de taille 3x3. En d'autres termes, le nombre d'éléments contenus dans l'ensemble 2B n'a pas été modifié alors que la taille l'était. Ceci nous conduit à proposer une autre définition basée sur l'opération de dilatation.

Définition 66 Soit B, un ensemble discret, fini de $\mathbb {Z}$ ² et de taille unitaire. On crée une famille d'objets binaires générée par B et caractérisée par le paramètre n = 0, 1, ... par

nB = $\displaystyle \underbrace{{B\oplus \ldots\oplus B}}_{{n-1\textrm{ dilatations}}}^{}\,$

(9.4)

Dans cette expression, nB est obtenu par (n - 1) dilatations successives. Si n = 0, 0B = {(0, 0)} par convention. Notons au passage que nB $\oplus$ mB = (n + m) $\oplus$ B pour tout n, m. Si B est convexe, alors nB a exactement la géométrie de B mais est de taille n. Remarquons que cette dernière définition est aussi valable pour des ensembles B convexes et continus.

9.1.3.3.3 Remarque pratique concernant l'implémentation.

Le théorème suivant permet d'arriver à une simplification de la formule 9.4.

Théorème 67 [39, page 132] Soit $\partial$ (B) la frontière du fermé B de $\mathbb {R}$ ². Alors

$\displaystyle \partial$ (B) $\displaystyle \oplus$ B = B $\displaystyle \oplus$ B

(9.5)

Dès lors,

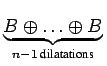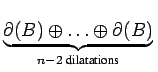nB = $\displaystyle \underbrace{{B\oplus \ldots\oplus B}}_{{n-1\textrm{ dilatations}}}^{}\,$ = B $\displaystyle \oplus$ $\displaystyle \underbrace{{\partial(B)\oplus \ldots\oplus \partial(B)}}_{{n-2\textrm{ dilatations}}}^{}\,$

(9.6)

Remarquons que cette formule donne un sorte de borne maximale. En effet, comme le montre le théorème suivant, il n'est pas nécessaire de prendre tous les points de la frontière lorsque la condition de réduction est respectée.

Théorème 68 [Condition de réduction] [39, page 130] Si A $\subseteq$ B alors

A $\displaystyle \oplus$ B $\displaystyle \supseteq$ B $\displaystyle \oplus$ B $\displaystyle \Leftrightarrow$ A $\displaystyle \oplus$ B = B $\displaystyle \oplus$ B

(9.7)

Pour s'en convaincre, prenons le cas d'un ensemble B = H $\oplus$ V. Alors B $\oplus$ B = B $\oplus$ $\partial$ (H) $\oplus$ $\partial$ (V); la condition de réduction est respectée si A = $\partial$ (H) $\oplus$ $\partial$ (V). Il suffit donc de dilater un rectangle B par ses quatre extrémités pour obtenir B $\oplus$ B.

La figure 9.10 illustre un autre cas.

**Figure 9.10:** Ici, $\partial$ (B) $\oplus$ B = ([a, b] $\cup$ {c}) $\oplus$ B.

9.1.3.3.4 Filtres multirésolution.

Définition 69 On définit l'ouverture et la fermeture à multirésolution par

X`o`nB	=	(X $\displaystyle \ominus$ nB) $\displaystyle \oplus$ nB	(9.8)
X $\displaystyle \bullet$ nB	=	(X $\displaystyle \oplus$ nB) $\displaystyle \ominus$ nB	(9.9)

Comme (X $\ominus$ B) $\ominus$ C = X $\ominus$ (B $\oplus$ C) et (X $\oplus$ B) $\oplus$ C = X $\oplus$ (B $\oplus$ C), l'ouverture s'exprime aussi par

XonB = [ $\displaystyle \underbrace{{(X\ominus B)\ominus B...\ominus B]}}_{{\textrm{n }\acute{\textrm{e}}\textrm{rosions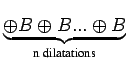}}}^{}\,$ $\displaystyle \underbrace{{\oplus B\oplus B...\oplus B}}_{{\textrm{n dilatations}}}^{}\,$ (9.10)

Une forme similaire vaut pour la fermeture X $\bullet$ nB. La complexité de cette dernière expression est directement proportionnelle au nombre de points de B alors que celle de (X $\ominus$ nB) $\oplus$ nB est de complexité quadratique. Si B a une forme suffisamment régulière, XonB et X $\bullet$ nB fournissent des versions filtrées non linéaires et multirésolution de la frontière de X. Par définition,

XonB = 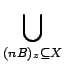$\displaystyle \bigcup_{{(nB)_{z}\subseteq X}}^{}$ (nB)_z (9.11)

Ainsi, XonB supprime toute la surface intérieure qui ne peut inclure un translaté de nB. C'est pour cette raison que l'on associe le concept de taille n à celle de l'objet analysé.

9.1.3.4 Définition formelle du squelette

Si en chaque point du squelette, on dessine le disque de taille maximale correspondant, l'union de ces cercles reconstitue l'objet de départ et l'enveloppe des disques formera le bord de l'objet. Soit S_r(X), r > 0, le sous-ensemble du squelette S(X) des centres des disques dont le rayon est égal à r; les sous-ensembles S_r(X) s'obtiennent par des opérations morphologiques d'érosion et d'ouverture. On peut démontrer qu'à l'exception des figures non bornées ou de celles incluant des points isolés, voire des lignes qui sont leur propre squelette, le squelette existe et s'exprime de manière équivalente par

S(X) = $\displaystyle \bigcup_{{r>0}}^{}$ S_r(X).

(9.12)

Bien que le concept de squelette soit difficile à étendre au cas d'images discrétisées, cela reste possible. SERRA propose une définition de la squelettisation qui s'applique à tout ensemble discret, borné et non vide. Nous passons à une définition plus pratique, due à LANTUÉJOUL, faisant intervenir les concepts de taille morphologique et de filtre multirésolution.

Définition 70 Le squelette d'un ensemble X s'obtient par l'union de sous-ensembles S_n, chacun de ces sous-ensembles étant l'ensemble des points de référence de copies de nB incluses dans X mais non incluses dans une copie de (n + 1)B contenue dans X

S_n(X) = (X $\displaystyle \ominus$ nB)\([X $\displaystyle \ominus$ nB]oB), n = 0, 1, ..., N (9.13)

S(X) = $\displaystyle \bigcup_{{n=0}}^{{N}}$ S_n(X)

(9.14)

où B est un carré de 2×2 pixels en trame carrée et un hexagone en trame hexagonale.

Les images représentées à la figure 9.11 ont été obtenues par le biais de cette formule.

Remarquons que la relation de LANTUÉJOUL fournit un squelette qui ne préserve pas la connexité.

Figure 9.11: Exemples de squelette tel que calculé par la formule de LANTUÉJOUL.

Le sous-ensemble de taille n, S_n(X), s'obtient en érodant X par nB, puis en ne conservant du résultat X $\ominus$ nB que les parties anguleuses et les lignes d'épaisseur nulle. Le squelette de taille n est la différence entre X $\ominus$ nB et son ouverture par B, (X $\ominus$ nB)oB. Si l'objet est entièrement contenu dans un masque de taille M×M, alors n $\leq$ M. De ces propos, il découle que la famille des couples (S_n(X), n) forme une description $\rho$ (X) de l'image. Pour obtenir une approximation $\pi$ (X) de l'image, il faut encore se munir d'une recomposition valable $\tau$ (X).

La squelettisation est une des rares transformations morphologiques à avoir un inverse. L'image numérisée X est reconstruite avec exactitude par la réunion de ses N + 1 sous-ensembles S_n(X) dilatés par l'élément de structure de taille adéquate:

$\displaystyle \pi$ (X) = X = $\displaystyle \bigcup_{{n=0}}^{{N}}$ [S_n(X) $\displaystyle \oplus$ nB]

(9.15)

Il apparaît clairement que plus l'indice n est élevé, plus les détails de reconstruction sont grossiers. Si on tient compte de l'associativité de la dilatation et de la distributivité de la dilatation par rapport à l'union, il est possible de trouver une forme équivalente de reconstruction de X

$\displaystyle \pi$ (X) = [[[S_N(X) $\displaystyle \oplus$ B] $\displaystyle \cup$ S_N-1(X)] $\displaystyle \oplus$ B $\displaystyle \cup$ S_N-2(X)...] $\displaystyle \oplus$ B $\displaystyle \cup$ S₀(X)

(9.16)

Nous avons vu que le squelette de X est plus mince que X par l'intermédiaire de la propriété d'anti-extensivité. De plus, les sous-ensembles S_n(X) forment une partition du squelette.

9.1.3.4.1 Autres formules.

Il existe d'autres formules de calcul de l'opération de squelettisation. VINCENT a proposé une méthode basée sur la fonction distance [41].

Définition 71 L'opérateur de fonction distance $\phi$ (X) d'un ensemble X $\subseteq$ $\mathcal {E}$ est la fonction définie par

[ $\displaystyle \phi$ (X)](h) = d (X^c, h)

(9.17)

avec la convention que d ( $\emptyset$ , h) = + $\infty$ pour h $\in$ $\mathcal {E}$ .

Par exemple, si on définit une image de marqueurs à partir des maxima locaux de la fonction distance, on obtient le squelette par boules maximales. Le principe de cet algorithme est illustré à la figure 9.12.

Figure 9.12: Squelette par boules maximales.


(a) Image binaire originale	(b) Courbes de niveau de la fonction distance

(c) Position des maxima locaux de (b)	(d) Squelette par boules maximales

La figure 9.13 montre quant à elle des squelettes calculés par l'algorithme de VINCENT. On voit que ce type d'algorithme préserve la connexité de la figure analysée.

Figure 9.13: Exemples de squelettes tels que calculés par l'algorithme de VINCENT.

Notes

...^9.1: Le terme ``discret'' est à prendre au sens de ``défini sur une grille d'échantillonnage'', tel qu'on le retrouve dans la littérature scientifique.