9.2.2 Indices de forme

Un premier moyen, très utilisé en pratique, pour caractériser une forme est d'inscrire l'objet dans un rectangle, un cercle ou tout autre forme de référence; le principe en est illustré à la figure 9.18. Les paramètres de ces formes de référence caractérisent alors grossièrement l'objet analysé.

Figure 9.18: Un objet et différentes figures de référence exinscrites.

Ainsi, PARKER [25] définit la rectangularité d'un objet comme le rapport entre l'aire de l'objet et l'aire du plus petit rectangle exinscrit. La rectangularité est toujours inférieure à 1; elle vaut 1 pour un rectangle.

Plus généralement, un indice de forme est une description chiffrée de la forme d'un objet binaire. RUSS [29] définit une série d'indices de forme. En voici quelques-uns (cf. tableau 9.1). Soient A(X), P(X), D_min et D_max respectivement l'aire de X, le périmètre de X, le diamètre minimum de l'ellipse exinscrite à X et le diamètre maximum.

Tableau 9.1: Quelques indices de forme (d'après [29]).

Nom	Expression
Facteur de forme	${\frac{{4\pi A({X})}}{{P({X})^{2}}}}$
Circularité	${\frac{{4A({X})}}{{\pi D_{max}^{2}}}}$
Rapport d'aspect	${\frac{{D_{max}}}{{D_{min}}}}$

On peut aussi considérer des indices qui mesurent l'écart, encore appelé déficit, entre la forme d'un objet et une forme de référence. Ainsi, on définit l'indice d'écart au cercle inscrit (de rayon R) comme

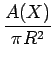$${\frac{{A({X})}}{{\pi R^{2}}}}$$ (9.20)