Sous-sections

9.2.4 Mesures morphologiques

Les mesures morphologiques les plus courantes sont des granulométries qui représentent l'évolution d'une caractéristique en fonction de la taille de l'élément structurant considéré pour l'analyse.

9.2.4.1 Granulométries

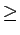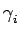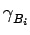Proposition 74   [12, page 93] Si Bi, i > 0, est une collection d'éléments structurants tels que Bi est égal à son ouvert au moyen de tout élément Bj si i $ \geq$ j, alors les ouvertures $ \gamma_{{i}}^{}$ = $ \gamma_{{B_{i}}}^{}$ satisfont la propriété de semi-groupe

$\displaystyle \gamma_{{i}}^{}$$\displaystyle \gamma_{{j}}^{}$ = $\displaystyle \gamma_{{j}}^{}$$\displaystyle \gamma_{{i}}^{}$ = $\displaystyle \gamma_{{i}}^{}$,       i $\displaystyle \geq$ j (9.24)

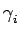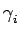Une collection de telles ouvertures $ \gamma_{{i}}^{}$, i > 0 est appelée granulométrie. La mesure de LEBESGUE des ensembles ouverts -l'aire en pratique- $ \gamma_{{i}}^{}$(X) définit une fonction décroissante de i > 0, appelée courbe granulométrique.

9.2.4.2 Covariogramme géométrique

Comme autre mesure morphologique, on peut définir le covariogramme qui effectue une mesure corrélatoire spatiale de l'objet.

Définition 75   [Covariogramme]

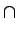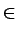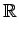CX(h) = A(X $\displaystyle \cap$ Xh)  pourh $\displaystyle \in$ $\displaystyle \mathbb {R}$2 (9.25)

L'emploi d'une telle mesure se justifie en présence de plusieurs objets non connexes et de forme fort proche, car le covariogramme fait ressortir l'écart entre les objets.

9.2.4.3 Enveloppe convexe

La notion de convexité et d'enveloppe convexe intervient souvent en traitement d'images. La convexité se définit de la manière suivante:

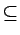
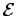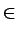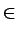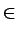Définition 76   [Convexité] Un ensemble X $ \subseteq$ $ \mathcal {E}$ est convexe si rx + (1 - r)y $ \in$ X pour tout x, y $ \in$ X avec r $ \in$ [0, 1].

Autrement dit, toute droite reliant deux points quelconques de X doit être entièrement contenue dans X. La figure 9.19 montre quelques objets.

Figure: A, B sont convexes; C ne l'est pas.
8553  

La notion de convexité permet de définir celle d'enveloppe convexe.

Définition 77   L'enveloppe convexe d'un ensemble X 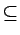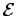$ \subseteq$ $ \mathcal {E}$, notée co(X), est l'intersection de tous les ensembles convexes contenant X.

La figure 9.20 montre un ensemble et son enveloppe convexe. Il est à remarquer que l'enveloppe convexe ne contiendra aucun trou, ce qui signifie que tous les trous de l'ensemble X seront bouchés.

Figure 9.20: Un ensemble X et son enveloppe convexe.
8569  

La convexité est une notion géométrique riche qui a donné naissance à des développements mathématiques intéressants. Le résultat suivant est une conséquence directe d'un théorème de CARATHEODORY.

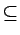
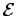
Proposition 78   [12, page 274] Soient X, Y $ \subseteq$ $ \mathcal {E}$

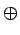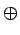co(X $\displaystyle \oplus$ Y) = co(X) $\displaystyle \oplus$ co(Y) (9.26)

Bien entendu, on peut définir des indices de forme basé sur l'enveloppe convexe. Ainsi, l'indice de convexité vaut

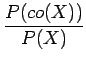$\displaystyle {\frac{{P({co(X)})}}{{P({X})}}}$ (9.27)

Marc Van Droogenbroeck. Tous droits réservés.
2003-09-30