Sous-sections
Le cas des images binaires est introduit en premier lieu. Il sera
plus aisé de généraliser ensuite le principe à des fonctions.
Soit X une image binaire. Cette image contient une série de zones
d'attraction centrées autour d'une famille de petits ensembles connexes
Zi. Le bassin associé au petit ensemble Zi est le sous-ensemble
de
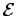 dont la distance géodésique à Zi est plus
petite que celle à Zj. Pour parler de distance géodésique, nous
introduisons quelques définitions et notations:
dont la distance géodésique à Zi est plus
petite que celle à Zj. Pour parler de distance géodésique, nous
introduisons quelques définitions et notations:
Parmi tous les chemins, le plus court détermine la distance géodésique.
La figure 10.4 fournit un exemple de
chemin géodésique.
Figure 10.4:
Le plus court chemin géodésique entre x et y.
|
|
Définition 82
[Distance géodésique] La distance géodésique
entre les points s et t est la longueur du plus court chemin
géodésique reliant s à t; elle est infinie si un tel chemin
n'existe pas.
Notations
La zone d'influence de l'ensemble Zi est notée
ZI(domaine =X,
centre = Zi) et sa frontière
FR(domaine =X,
centre = Zi).
Le squelette par zone d'influence
(SZI) s'obtient aisément par l'algorithme suivant:
- dans un premier temps, on délimite les zones Zi des régions
de base;
- pour les autres pixels, il suffit d'itérer la démarche suivante jusqu'à
stabilisation du processus: si un pixel a un voisin indicé i, alors
ce pixel prend le même indice; les points qui n'ont pas de voisin
ou ceux qui en ont deux sont laissés inchangés;
- au terme de ce processus, les pixels sont attribués à l'une ou l'autre
zone de départ Zi.
Cet algorithme simple revient à faire croître des régions jusqu'à
ce qu'elles se touchent; de la sorte, les contours obtenus sont fermés.
La figure 10.5 montre un exemple de squelette géodésique.
Figure 10.5:
Squelette géodésique.
|
|
Supposons que le relief soit progressivement immergé, l'incrément
étant d'une unité de luminance par étape. C'est la clef de synthèse
d'un algorithme de détermination de ligne de séparation. Le dessin
de la figure 10.6 montre une étape intermédiaire du processus
d'immersion.
Figure 10.6:
Construction d'un barrage au raccord de deux bassins versants.
|
|
- f est la fonction étudiée.
- hmin et hmax sont les valeurs extrêmes de f
sur son domaine de définition.
-
Th(f )= {x
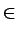 dom f : f (x)
dom f : f (x) 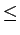 h} est l'ensemble
constitué par un seuil h.
h} est l'ensemble
constitué par un seuil h.
- Mi sont les minima et
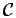 (Mi) les bassins
correspondants.
(Mi) les bassins
correspondants.
Les bassins seront construits étape par étape suite à une augmentation
progressive du niveau de l'eau. Soit
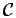 h(Mi) la
partie du bassin Mi rempli au temps algorithmique h. Alors
h(Mi) la
partie du bassin Mi rempli au temps algorithmique h. Alors
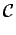 h(Mi) = h(Mi) = 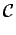 (Mi) (Mi) 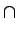 Th(f ) Th(f ) |
(10.3) |
Dans cette expression,
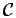 (Mi) est l'inconnue. Si l'altitude
du minimum Mi est j, alors
(Mi) est l'inconnue. Si l'altitude
du minimum Mi est j, alors
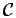 j(Mi) = Mi
et
j(Mi) = Mi
et
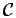 k(Mi) =
k(Mi) = 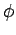 pour k < j. L'union de tous les
bassins est notée
pour k < j. L'union de tous les
bassins est notée
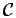 (M) et sa partie immergée au temps
h est
(M) et sa partie immergée au temps
h est
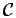 h(M). Dans ces conditions,
h(M). Dans ces conditions,
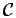 h max(M) =
h max(M) = 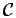 (M).
Il reste à initialiser l'algorithme et à donner un schéma de construction.
Attention, il n'est pas question ici de supprimer des faux bassins.
(M).
Il reste à initialiser l'algorithme et à donner un schéma de construction.
Attention, il n'est pas question ici de supprimer des faux bassins.
-
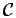 h min(M) = Th min(f ); l'initialisation
considère que tous les points minima sont des réservoirs potentiels.
h min(M) = Th min(f ); l'initialisation
considère que tous les points minima sont des réservoirs potentiels.
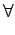 h h 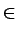 [hmin +1, hmax] : [hmin +1, hmax] : 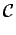 h(M) = ZIh h(M) = ZIh 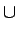 Minh Minh |
(10.4) |
avec
- ZIh = zone d'influence (de domaine Th(f )) composée des
centres contenus dans
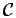 h-1(M) -c'est durant cette
étape que seront déterminés les barrages traduits en contours;
h-1(M) -c'est durant cette
étape que seront déterminés les barrages traduits en contours;
- Minh est l'ensemble des points de Th(f ) qui, après le
processus de recherche de zones d'influence n'ont toujours pas de
voisin. Il s'agit de nouveaux minima, centres de nouvelles zones d'influence.
Cet algorithme peut subir quelques modifications destinées à supprimer
les faux contours; des développements de ce type sont abondamment
décrits par MEYER (le véritable initiateur de ces techniques)
et BEUCHER [21]. MEYER a également développé
une recherche de lignes de séparation entre bassins par analogie avec
l'opération de squelettisation légèrement modifiée; de telles considérations
nous mèneraient malheureusement trop loin. Remarquons simplement que
l'algorithme développé est relativement complexe et que, dès lors,
il n'est guère étonnant que certains auteurs (cf. [34]
par exemple) aient développé des expressions plus agréables.
Le remède communément adopté pour combattre la sur-segmentation est
le marquage. Dans le cas présent, le marquage
consiste à sélectionner certains minima seulement. On part de la constatation
que le nombre de régions est généralement proportionnel au nombre
de minima. Le fait de ne sélectionner qu'une partie des minima entraîne
la disparition de certaines régions. En effet, lors du processus d'inondation,
ces régions sont remplies par l'eau provenant d'un bassin voisin en
passant par le point de crête ayant la plus faible altitude. Les bassins
inondés sont alors englobés dans un bassin voisin.
Les avantages de la ligne de partage des eaux par rapport à d'autres
techniques de segmentation se résument en définitive à
- la possibilité de travailler sur base d'une image de gradient quelconque,
- la possibilité d'effectuer une pré-sélection par un marquage adéquat.
Marc Van Droogenbroeck. Tous droits réservés.
2003-09-30
![]() dont la distance géodésique à Zi est plus
petite que celle à Zj. Pour parler de distance géodésique, nous
introduisons quelques définitions et notations:
dont la distance géodésique à Zi est plus
petite que celle à Zj. Pour parler de distance géodésique, nous
introduisons quelques définitions et notations:
![]() (Mi) est l'inconnue. Si l'altitude
du minimum Mi est j, alors
(Mi) est l'inconnue. Si l'altitude
du minimum Mi est j, alors
![]() j(Mi) = Mi
et
j(Mi) = Mi
et
![]() k(Mi) =
k(Mi) = ![]() pour k < j. L'union de tous les
bassins est notée
pour k < j. L'union de tous les
bassins est notée
![]() (M) et sa partie immergée au temps
h est
(M) et sa partie immergée au temps
h est
![]() h(M). Dans ces conditions,
h(M). Dans ces conditions,
![]() h max(M) =
h max(M) = ![]() (M).
Il reste à initialiser l'algorithme et à donner un schéma de construction.
Attention, il n'est pas question ici de supprimer des faux bassins.
(M).
Il reste à initialiser l'algorithme et à donner un schéma de construction.
Attention, il n'est pas question ici de supprimer des faux bassins.